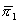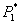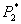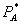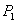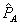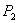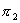An Antitrust Analysis Of Bundled Loyalty Discounts
AN ANTITRUST ANALYSIS OF
BUNDLED LOYALTY DISCOUNTS
by
Patrick Greenleea
David Reitmanb
David S. Sibleyc
October 30, 2006
Abstract
Consider a monopolist in one market that faces competition in a second market. Bundled loyalty discounts, in which customers receive a price break on the monopoly good in exchange for making all purchases from the monopolist, have ambiguous welfare effects. To analyze such discounts as predatory pricing is incorrect. In some settings, they act as tie-in sales. Existing tests for whether such discounts violate Section 2 of the Sherman Act do not track changes in consumer surplus or total surplus. We present a new test and use it in an illustrative example based on SmithKline that assumes the “tied” market is a homogeneous good. If the tied market is characterized by Hotelling competition, bundling by the monopolist causes the rival firm to reduce its price. In numerical examples, we find that this can deter entry or induce exit.
JEL Code: L42
Keywords: market share discount; bundling; tying; predation
I. INTRODUCTION
Bundled loyalty discounts provide price breaks on one or more products to buyers that remain sufficiently loyal to a supplier. They resemble volume discounts in that shifting incremental purchases from a rival supplier may allow a buyer to satisfy a loyalty requirement and thereby enjoy lower prices. They resemble tying when affordable prices for one (tying) product are available only to consumers that are completely loyal to the supplier in their purchases of a second (tied) product. Like volume discounts and tying, bundled loyalty discounts can enhance or diminish consumer surplus and total welfare by improving the ability to price discriminate, and they can change the long run incentives for single-product firms to enter/exit. Open questions include under what conditions should competition authorities treat bundled loyalty discounts like tying or predatory pricing, and when do bundled rebates enhance welfare.
Bundled loyalty discounts have recently received considerable attention in antitrust circles in light of LePage’s, Inc. et al. v. 3M Company,[1] Michelin v. Commission,[2] and a number of pending court cases.[3] Until recently, the practice of bundled rebates has received comparatively little scholarly and judicial scrutiny. Indeed, only a small number of cases litigated in the U.S. have focused squarely on these practices, including SmithKline Corp. v. Eli Lilly & Co.[4] and Ortho Diagnostics Sys., Inc. v. Abbott Lab, Inc.[5] Virgin Atlantic Airways Ltd. v. British Airways PLC[6] involved similar practices, but the district court found allegations of anticompetitive behavior to be unsupported by fact. LePage’s provides a good background for the issues involved.
The facts in LePage’s begin with the very strong brand name of Scotch tape, a 3M product. Most retail merchants believed that they had to offer Scotch tape. Until the early 1990’s, 3M’s share of the U.S. market for transparent and invisible tape exceeded 90%. Starting in the early 1990’s, however, 3M’s share began to erode with the rise of office superstores such as Staples and Office Depot. These retailers sold products, including tape, under their own names as private labels. LePage’s dominated the growing private label segment, with an 88% market share in 1992. Its share of the overall tape market, however, was only 14%.
3M responded by adding a private label of its own, under the Highland name. 3M’s entry involved the use of a bundled rebate program that “offered discounts to certain customers conditioned on purchases spanning” multiple product lines, with the size of the rebate depending on the extent to which the customer met growth targets established by 3M. 3M’s bundled discounts apparently proved successful in shifting a large fraction of private label tape business to 3M. In 1992, LePage’s filed a four-count antitrust suit against 3M that was ultimately narrowed to a monopolization claim under Section 2 of the Sherman Act.[7] LePage’s argued that it was foreclosed from selling private label tape because it could not cover its costs and still compensate customers for the rebates lost on other products in the discount program when the customer bought private label tape from LePage’s instead of from 3M.
The legal strategy of the defendant, 3M, was to compare price to cost and use the case law of predation. It argued that as long as the price of each item in its bundle exceeded cost, the pricing scheme was legal. In other words, 3M argued that the relevant case law was that of predatory pricing, as presented in Brooke Group.[8] In its appellate filings, 3M used a different approach, the Ortho test. In Ortho, the defendant offered bundled discounts on products,[9] some of which were competitive and some of which were monopoly products due to patents. The Court allocated the total bundle rebate to the competitive product in question and compared that globally discounted price to the defendant’s cost. This approach effectively adapted Brooke Group to the analysis of bundled discounts. According to this test, if the discount-adjusted price of the competitive product exceeds its cost, then the bundled discount pricing strategy is deemed not anti-competitive.
The great interest in LePage’s probably stems from the fact that bundled rebates are a widespread business practice. Until LePage’s, the Ortho test was an accepted way of analyzing bundled discounts. The Court of Appeals’ decision in LePage’s, however, leaves matters in doubt. To quote the U.S. Department of Justice:
Employing a bundled loyalty discount imposes switching costs on customers because a customer that shifts some purchases to a rival seller pays a higher unit price for the quantity still purchased from the incumbent. In VAA/BA, Virgin Atlantic proposed an incremental sales test to judge the legality of such pricing plans. This test compares the competitor’s incremental revenue from making those new sales to the customer to the competitor’s incremental cost. Because the competitor must compensate the customer for the switching cost, net incremental revenue may be forced below incremental cost. In such a setting, “incremental” competition is unprofitable and is deterred by the loyalty discount plan. The VAA/BA test simply checks whether net incremental revenue exceeds incremental cost, and if it does, the loyalty discount plan is presumed legal. Like Ortho, this test analyzes bundled rebates using predation case law.
The academic economics literature on bundled discounts is rather sparse. Bundling for the purpose of price discrimination has a large literature, but usually in a monopoly setting. The main exception is Nalebuff (2004a), who has written extensively on how bundling can be used to reduce competition. Discounts that apply to every unit purchased have a smaller literature. Kolay, Shaffer, and Ordover (2004) examine a monopolist’s use of all-units discounts on a single product, and compare them to menus of two-part tariffs. Greenlee and Reitman (2004) analyze loyalty discounts, both with and without bundling. In a duopoly differentiated products setting in which both firms can offer a loyalty program to a retailer that sells to consumers with varying tastes, they show that firms pass the VAA/BA test in equilibrium. Thus failing the VAA/BA test suggests that a firm has goals other than short-term profit maximization. In a setting similar to LePage’s, they show that the introduction of bundled discounts causes standalone prices to rise. The welfare effects of bundled rebates in Greenlee and Reitman (2004) are ambiguous, since their models allow for price discrimination across consumer types.[11] Nalebuff (2004b, 2005) together contain results similar to Theorems 1 and 2 below, under the assumption that the tied market is perfectly competitive. We relax this assumption in part of our analysis.
From the standpoint of antitrust enforcement, it is unclear what body of case law best applies to bundled discounts. The approaches of the Ortho test and the VAA/BA incremental test suggest that bundled rebates should be analyzed as a method of predation. In LePage’s, 3M argued vigorously in its appellate briefs that its discounts were legal under Brooke Group because even its discounted prices were above cost, an assertion not challenged by the plaintiff.
However, because the intent of bundling is to induce consumers to buy multiple products from a single seller, perhaps tying is a more appropriate way to look at bundled discounts. Indeed, the Third Circuit suggested this in LePage’s, but went no further. It is worth noting that in LePage’s and in Ortho, the firm offering the loyalty program included in the bundle a product over which it had either a monopoly (Ortho, due to patents) or a very strong brand name (Scotch tape, in LePage’s). Monopoly goods within the bundle, then, may play the role of tying products. As we show below, however, bundled discounts are not always equivalent to tying.
While our focus is on the short term competitive effects of bundled loyalty discounts, a full analysis of bundled rebates would also consider the longer term implications as new competitors contemplate entry and/or incumbent competitors consider exit. Similar to tying, bundled rebates can change the terms on which firms compete in the linked market. As we will discuss, however, the manner in which bundled rebates influence the dynamics of competition differ from the effects of tying.
To summarize, this paper provides preliminary answers to two main questions. First, what is the correct legal framework to use in the antitrust analysis of bundled loyalty discounts? Second, how can one distinguish between bundled discounts that benefit consumers from ones that do not?
We reach the following conclusions.
- When the tied market is perfectly competitive, bundled discounts resemble tying and are not a form of predatory pricing.
- Bundled discounts can raise or lower consumer welfare. In either case, equally efficient competitors may be foreclosed. Profit-maximizing bundled discounts lower consumer surplus when the tied market is perfectly competitive.
- If products in the tied market are homogeneous, simple price comparison tests exist that can distinguish bundled rebates that raise consumer surplus from those that do not.
- These tests, applied to SmithKline, suggest that the bundled discounts at issue there probably lowered consumer surplus and total surplus.
- If the rivalrous market is a differentiated product duopoly rather than characterized by homogeneous goods, bundled discounts are not equivalent to tying. In such cases, profit-maximizing loyalty programs have ambiguous welfare effects, and aggregate consumer surplus can rise or fall due to bundling. This suggests that bundled discounts should not always be analyzed as tying arrangements.
- In the differentiated product setting, bundled discounts reduce rents for the non-bundling firm. Numerical examples indicate that bundled discounts can deter entry or induce exit.
The remainder of this article is organized in the following manner. Section II introduces our base model of a monopolist in one market that faces perfect competition in a second market. Sections III and IV discuss existing tests of bundled discounts and introduce a generalized test. Section V applies this test to SmithKline. Section VI briefly looks at nonlinear pricing and establishes that a monopolist benefits from offering a menu of bundled “three-part tariffs” that is not feasible without bundling. Section VII modifies the initial model by making the second market a differentiated duopoly. Section VIII concludes.
II. MODEL 1: PERFECT COMPETITION IN THE LINKED MARKET
Firm 1 has a monopoly in market A and is one of many perfect competitors in market B. For each consumer, demands are economically independent and described by 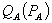 and
and 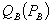 . All consumers demand B, though some consumers may have zero demand for A at any positive price. Non-zero demands are assumed to be downward sloping. As in LePage’s, firm 1 signs a contract with each consumer that specifies bundled rebates, or fails to do so. Absent signing a contract, the consumer buys A at the standalone price and B at marginal cost.
. All consumers demand B, though some consumers may have zero demand for A at any positive price. Non-zero demands are assumed to be downward sloping. As in LePage’s, firm 1 signs a contract with each consumer that specifies bundled rebates, or fails to do so. Absent signing a contract, the consumer buys A at the standalone price and B at marginal cost.
Let 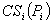 be consumer surplus, where
be consumer surplus, where 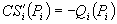 ,
, 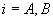 . Denote by
. Denote by 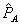 the choke price for market A, given by
the choke price for market A, given by 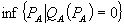 , and let
, and let 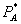 and
and 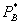 be the standalone monopoly prices in markets A and B. Firm A has constant marginal cost
be the standalone monopoly prices in markets A and B. Firm A has constant marginal cost 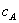 for A and all firms have constant marginal cost
for A and all firms have constant marginal cost 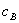 for B.
for B.
An important assumption throughout is that consumer surplus is positive in market A at the monopoly price. This rules out the possibility that firm 1 extracts the entire consumer surplus via a two-part tariff. Less-than-full rent extraction can occur for a variety of reasons including contract incompleteness and demand uncertainty. When contracts cannot completely specify the terms of exchange, the joint surplus of the supplier and retailer depends on the parties’ relative bargaining power, so rent extraction typically is less than complete.[12] When demand for the monopoly product is stochastic, the optimal two-part tariff does not extract all expected surplus from market A. Under this interpretation,  can be thought of as an expected demand curve and
can be thought of as an expected demand curve and 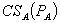 as expected consumer surplus.[13]
as expected consumer surplus.[13]
To establish terminology, a price pair 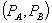 is a bundled loyalty discount if it is available to consumers only on the condition that they buy everything from firm 1. Firm 1 also sets a standalone price for A, which a consumer pays if he or she buys B from a competitor. The price of A in the bundle is discounted from the standalone price. We imagine an initial situation in which firm 1 prices independently across markets, setting prices at
is a bundled loyalty discount if it is available to consumers only on the condition that they buy everything from firm 1. Firm 1 also sets a standalone price for A, which a consumer pays if he or she buys B from a competitor. The price of A in the bundle is discounted from the standalone price. We imagine an initial situation in which firm 1 prices independently across markets, setting prices at 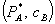 . Subsequently, firm 1 offers a bundled discount plan, consisting of bundled prices and a standalone price for A. This paper studies the effects of this pricing innovation.
. Subsequently, firm 1 offers a bundled discount plan, consisting of bundled prices and a standalone price for A. This paper studies the effects of this pricing innovation.
We consider, in turn, independent pricing by the monopolist and a loyalty program that consists of a standalone price 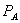 and a price pair
and a price pair 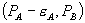 . A consumer that participates in the loyalty program receives an
. A consumer that participates in the loyalty program receives an 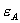 discount on all its purchase of A whenever it agrees to make all of its B purchases (at price
discount on all its purchase of A whenever it agrees to make all of its B purchases (at price 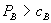 ) from firm 1. Faced with these alternatives, the consumer decides whether to participate in the bundled rebate program and makes purchases accordingly.
) from firm 1. Faced with these alternatives, the consumer decides whether to participate in the bundled rebate program and makes purchases accordingly.
- Pareto-Improving Bundled Rebates
One theme of this article is that bundled rebates, with or without a share-based loyalty feature, can improve or harm welfare. To see how welfare may increase, suppose that initially there is independent pricing, firm 1 charges 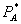 for A and
for A and 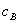 for B. Firm 1 can construct another pair of prices consisting of a slightly discounted price of A and a price of B slightly above
for B. Firm 1 can construct another pair of prices consisting of a slightly discounted price of A and a price of B slightly above 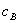 . We can write this price pair as
. We can write this price pair as 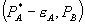 . For
. For  close enough to
close enough to 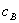 , consumers prefer this pair to
, consumers prefer this pair to  . Furthermore, since the effect of
. Furthermore, since the effect of 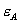 on profits is second-order, but that of
on profits is second-order, but that of 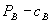 is first-order, firm 1’s profit increases. If firm 1 makes
is first-order, firm 1’s profit increases. If firm 1 makes 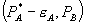 available only to consumers who buy entirely from firm 1, then
available only to consumers who buy entirely from firm 1, then  is a bundled rebate. Note that because the consumer prefers the bundled rebate to the initial (and still available) prices, an equally efficient competitor cannot make sales of B at price equal to
is a bundled rebate. Note that because the consumer prefers the bundled rebate to the initial (and still available) prices, an equally efficient competitor cannot make sales of B at price equal to 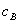 .
.
To develop intuition, we first consider introducing bundled rebates  under the assumption that the standalone price for A remains at the monopoly level. In the subsection that follows this initial development, we allow the monopolist also to adjust the standalone price. When the standalone price remains at the monopoly level, the optimal loyalty discount program
under the assumption that the standalone price for A remains at the monopoly level. In the subsection that follows this initial development, we allow the monopolist also to adjust the standalone price. When the standalone price remains at the monopoly level, the optimal loyalty discount program 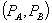 maximizes firm 1 profit subject to the constraint that consumer surplus at
maximizes firm 1 profit subject to the constraint that consumer surplus at 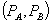 weakly exceeds consumer surplus at
weakly exceeds consumer surplus at 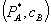 . Formally, the monopolist’s objective is to
. Formally, the monopolist’s objective is to
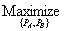
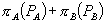 (1)
(1)
subject to: 
Without loss of generality, we assume that if the incentive compatibility restraint is met with equality, the consumer selects the bundled rebate program.
Theorem 1: [Pareto Improvement] Letting  denote the optimal program prices, the solution to (1) has the following features:
denote the optimal program prices, the solution to (1) has the following features:
(1) 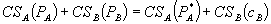 .
.
(2)  .
.
(3) Total surplus at 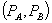 exceeds total surplus at
exceeds total surplus at 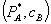 .
.
(4) 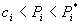 ,
, 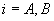 .
.
(5) Equally efficient competitors are foreclosed in market B.
Proof. See Appendix.
This theorem has three implications. First, it shows that the effect of bundled rebates for antitrust analysis is not akin to predation. Not only do 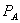 and
and 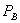 exceed marginal cost, but there is no short run profit sacrifice, as called for by Brooke Group. Nevertheless, equally efficient competitors are foreclosed: the lost discount on A exceeds the benefit received from obtaining B at price
exceed marginal cost, but there is no short run profit sacrifice, as called for by Brooke Group. Nevertheless, equally efficient competitors are foreclosed: the lost discount on A exceeds the benefit received from obtaining B at price 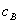 instead of
instead of 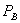 . Second, although foreclosure is often discussed as reducing welfare, this need not hold for bundled rebates. Third, bundled rebates are equivalent to tie-in sales in this setting. The “standalone” price
. Second, although foreclosure is often discussed as reducing welfare, this need not hold for bundled rebates. Third, bundled rebates are equivalent to tie-in sales in this setting. The “standalone” price 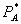 serves only to induce consumers to select the bundled prices and buy everything from firm 1.
serves only to induce consumers to select the bundled prices and buy everything from firm 1.
- Monopoly Extension Using Bundled Rebates
We now consider how bundled rebates can extend monopoly from A to B. Firm 1 sets a standalone price for A, 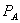 , a discount
, a discount  , and also sets a price
, and also sets a price 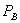 for B. The prices
for B. The prices  are only available if the consumer buys everything from firm 1. Otherwise, the consumer pays
are only available if the consumer buys everything from firm 1. Otherwise, the consumer pays 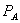 to buy A from firm 1 and buys B from a competitor at price
to buy A from firm 1 and buys B from a competitor at price 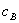 . Firm 1’s objective is to
. Firm 1’s objective is to
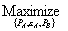
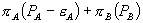 (2)
(2)
subject to: 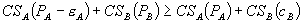
Observe that in this setting, the standalone price 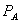 can be set arbitrarily high provided that
can be set arbitrarily high provided that 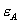 increases in a similar fashion. As
increases in a similar fashion. As 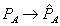 ,
, 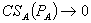 and the incentive compatibility constraint in this problem converges to that of a straight requirements tying problem.[14]
and the incentive compatibility constraint in this problem converges to that of a straight requirements tying problem.[14]
If  then the constraint above is slack at the optimum. The bundled rebate is
then the constraint above is slack at the optimum. The bundled rebate is 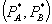 and
and 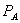
 can be set so that
can be set so that
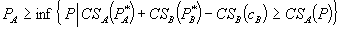 (3)
(3)
If 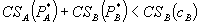 then the constraint binds at the optimum and
then the constraint binds at the optimum and 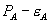 and
and  are set below their monopoly levels. In equilibrium,
are set below their monopoly levels. In equilibrium, 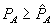 in order to relax the incentive constraint as much as possible. With this, the problem is akin to a requirements tying problem, but monopoly extension is not complete. The following theorem summarizes this discussion.
in order to relax the incentive constraint as much as possible. With this, the problem is akin to a requirements tying problem, but monopoly extension is not complete. The following theorem summarizes this discussion.
Theorem 2: [Monopoly Extension] Consider the loyalty discount 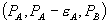 .
.
- If
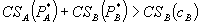 , then
, then  ,
,  , and
, and
 .
. - If
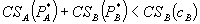 , then
, then 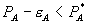 ,
,  , and
, and  .
.
Notice that equally efficient competitors are foreclosed again, and employing a bundled rebate reduces consumer welfare. In Theorem 2.i, total surplus declines because the bundled rebate generates a deadweight loss in B and no change in A.
Note that in Theorem 2.ii, where 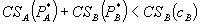 , the profit maximizing price of A,
, the profit maximizing price of A,  , is below the initial monopoly price,
, is below the initial monopoly price, 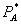 . One might conjecture that consumer welfare increases because the effective price of A has fallen. For Theorem 2.ii, however, the optimal prices constrain consumer welfare to equal
. One might conjecture that consumer welfare increases because the effective price of A has fallen. For Theorem 2.ii, however, the optimal prices constrain consumer welfare to equal 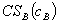 . In contrast, consumer welfare equals
. In contrast, consumer welfare equals 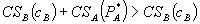 under independent pricing. Hence, using a bundled rebate reduces consumer welfare, even though the price of A has fallen.
under independent pricing. Hence, using a bundled rebate reduces consumer welfare, even though the price of A has fallen.
The total surplus effect of bundled discounts, however, is ambiguous. Compared to the independent prices 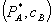 , in Theorem 2.ii the bundled price of A is lower and that of B is higher. Hence, total surplus rises or falls depending on the relative market demands. The following corollary provides additional precision for the case of linear demands in both markets.
, in Theorem 2.ii the bundled price of A is lower and that of B is higher. Hence, total surplus rises or falls depending on the relative market demands. The following corollary provides additional precision for the case of linear demands in both markets.
Corollary 1. Suppose demands and costs are linear in both markets.
(i) Theorem 2.i corresponds to the inequality: 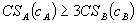 .
.
(ii) If 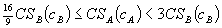 , then Theorem 2.ii applies and bundled discounts lower total surplus.
, then Theorem 2.ii applies and bundled discounts lower total surplus.
(iii) If 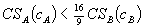 , then Theorem 2.ii applies and bundled discounts increase total surplus.
, then Theorem 2.ii applies and bundled discounts increase total surplus.
Proof: See Appendix.
For ease of exposition, we have assumed no uncertainty in the demand curves for A and B. With this modeling simplification, bundled discounts are unnecessary whenever the monopolist can set a two-part tariff that extracts all surplus in A. As Mathewson and Winter (1997) establish, however, tying can improve profits when demands for A and B are uncertain but correlated. With stochastic demand, the optimal two-part tariff does not extract all surplus in A, and tying allows the monopolist to flexibly extract additional consumer surplus when demand is high. In Section VI, we introduce uncertainty by having the consumer’s demand be a random variable (high or low) whose realization is unobserved by firms. If demand realizations for A and B satisfy non-crossing and uniform ordering properties, then firm 1 earns strictly greater profit when it offers a menu of bundled “three-part tariffs” (consisting of an entry fee, a discounted price for A, and a discounted price for B) than when it offers a menu of separate two-part tariffs for A and prices competitively in B. Thus with demand uncertainty, bundled discounts are not redundant to a monopolist that can offer two-part tariffs.[15]
The purpose of stating Theorems 1 and 2 separately is to provide a means of distinguishing bundled rebate plans that lower consumer welfare from those that do not. For example, one could compare the effective price of the monopoly good in the bundle to its price under a pre-existing independent pricing regime. If there is no difference, then the bundled rebate plan cannot be Pareto-improving, since Pareto-improving discount plans involve at least a small reduction in the price of the monopoly good (Theorem 1). Such a pattern of no price change for A would be consistent with Theorem 2.i. If the price of A in the bundle is lower than the pre-existing independent price, this is consistent with both Theorem 1 and Theorem 2. To distinguish between them, compare the standalone prices. Under Theorem 1, the standalone price is simply the pre-existing monopoly price, while under Theorem 2.ii the equilibrium standalone price is higher. The only cases left to consider involve the standalone price being less than 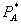 , which is not optimal for firm 1. Thus, even though the bundle price of B is above marginal cost, the net consumer effect is seen just by comparing
, which is not optimal for firm 1. Thus, even though the bundle price of B is above marginal cost, the net consumer effect is seen just by comparing 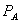 and
and  .[16] Naturally, applying these tests requires price data for well-defined periods preceding and following the introduction of bundled rebates.
.[16] Naturally, applying these tests requires price data for well-defined periods preceding and following the introduction of bundled rebates.
One may object that Theorem 1 is of little relevance because the monopolist can increase its profits by raising the standalone price above the initial monopoly price. The implication is that one would never expect to see a standalone price no higher than the pre-bundling monopoly price. One response is that, nonetheless, firms may behave in this manner. 3M, for example, claimed consistently that its bundled discount prices were all lower that its pre-bundling prices and that the standalone prices were simply the pre-bundling prices, with subsequent adjustments for cost increases.[17] At a minimum, if Model 1 applies, the condition  could be used as a safe harbor in antitrust enforcement.[18]
could be used as a safe harbor in antitrust enforcement.[18]
III. EXISTING TESTS OF BUNDLED REBATES
As argued above, bundled rebates are not equivalent to predation, so the case law involving Brooke Group is unlikely to be directly useful in antitrust enforcement. Rather, for settings resembling Model 1, bundled rebates are best viewed as a form of tie-in sale. That said, the case law on tying does not provide convenient rule of reason tests for the competitive effects of bundled rebates, and tying often has ambiguous welfare effects.
One test described above is the Ortho test. In our terminology, the Ortho test would ask whether firm 1’s revenues from B less the discounts on A cover its costs of B. If so, then the bundled rebates plan is presumed legal.[19] One problem with this test is that it assumes disequilibrium behavior. That is, if it is passed, why has not a market B competitor already undercut the bundle?[20]
Alternatively, competitors may have higher costs than firm 1, so that they cannot undercut in market B. This implies a different underlying model than the present one, and it is not clear that antitrust attention is warranted when rivals have higher costs. Thus, if the Ortho test is passed by firm 1, but rivals in market B cannot undercut firm 1’s price in market B, their lack of success may not result from firm 1’s pricing, but from their own cost disadvantages.
A second point to keep in mind is that a bundled discount program can fail the Ortho test yet still raise consumer surplus.[21] Consider again the intuition behind Theorem 1. Suppose the monopolist offers a loyalty discount program that prices A slightly below 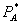 and B at marginal cost. To a first order, monopolist profits have not fallen and the consumer strictly prefers facing
and B at marginal cost. To a first order, monopolist profits have not fallen and the consumer strictly prefers facing  rather than
rather than  . Thus, total welfare and consumer welfare have risen. However, even for
. Thus, total welfare and consumer welfare have risen. However, even for  extremely small, a perfect competitor in B cannot “pay” the consumer
extremely small, a perfect competitor in B cannot “pay” the consumer 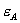 and still earn a non-negative profit. For these two reasons, the Ortho test cannot detect consumer surplus or total surplus changes. Nonetheless, it can be used as a safe harbor test.[22]
and still earn a non-negative profit. For these two reasons, the Ortho test cannot detect consumer surplus or total surplus changes. Nonetheless, it can be used as a safe harbor test.[22]
The VAA/BA incremental profit test also merits discussion. Share-based discounts can exist within a bundle of prices or can apply to an unbundled single product. Parsing the term “bundled rebates,” it appears that for homogenous goods it is the bundling of discounted prices that has importance for competition, not whether the discounted prices within the bundle are share-based. While a loyalty discount program may make it unprofitable for equally efficient competitors to win incremental business, such firms can compete effectively for the consumer’s entire requirements. Thus, with homogenous products, a bundled discount program can flunk the VAA/BA test, yet not reduce competition, consumer surplus, or total surplus. Hence, the usefulness of the VAA/BA incremental test in the present context appears limited.[23] By contrast, the price comparisons described above involve equilibrium prices and can distinguish bundled rebates that raise consumer welfare from those that lower it. Neither the Ortho test nor the VAA/BA test can do this, even in principle.
IV. EXTENSIONS AND VARIATIONS OF MODEL 1
- Non-Independent Demands
Our discussion has assumed independent demands for A and B. This facilitates characterizing the optimal bundled and standalone prices. For the more limited (but still important) purpose of determining whether a newly introduced bundled discount strategy raises or lowers consumer surplus, we do not need this assumption.
Suppose that the introduction of a bundled discount causes no change in the price of B. If the standalone price of A, 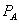 , is no higher than the pre-bundling monopoly price, then the outside options available to consumers are no worse than before the introduction of the bundled rebate. Consumer surplus cannot decline following the introduction of such a program. Clearly, this requires no special assumptions about whether A and B are complements, substitutes, or are independent.
, is no higher than the pre-bundling monopoly price, then the outside options available to consumers are no worse than before the introduction of the bundled rebate. Consumer surplus cannot decline following the introduction of such a program. Clearly, this requires no special assumptions about whether A and B are complements, substitutes, or are independent.
Suppose, alternatively, that the standalone price of A rises with the introduction of the bundled rebate. Since the price of B cannot fall below 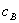 in equilibrium, this implies that the outside options available to consumers are less desirable than the initial prices
in equilibrium, this implies that the outside options available to consumers are less desirable than the initial prices  and
and  . The loyalty program that maximizes firm 1 profit makes the consumer indifferent between the bundle rebate prices
. The loyalty program that maximizes firm 1 profit makes the consumer indifferent between the bundle rebate prices  and the standalone prices
and the standalone prices 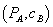 . Hence, if
. Hence, if  then introducing the bundled rebate reduces consumer surplus. Thus, assuming that firm 1 maximizes profits, we have a test to determine how bundled loyalty discounts affect consumer surplus: if
then introducing the bundled rebate reduces consumer surplus. Thus, assuming that firm 1 maximizes profits, we have a test to determine how bundled loyalty discounts affect consumer surplus: if  , consumer surplus weakly increases, and if
, consumer surplus weakly increases, and if 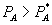 , consumer surplus diminishes.
, consumer surplus diminishes.
As a practical matter, one should sound a cautionary note about the second part of the test. To infer consumer harm from observing 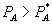 requires that firm 1 comes close to actually maximizing profits. If the firm fails to maximize profits, it could be true that
requires that firm 1 comes close to actually maximizing profits. If the firm fails to maximize profits, it could be true that 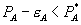 and
and  , but
, but 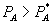 . Clearly, the consumer benefits, but since
. Clearly, the consumer benefits, but since  , our proposed test would suggest otherwise. Hence, before using
, our proposed test would suggest otherwise. Hence, before using  to infer anything, the analyst should try to verify that the bundling firm is maximizing profits. Alternatively, if the bundled price is sufficiently high that
to infer anything, the analyst should try to verify that the bundling firm is maximizing profits. Alternatively, if the bundled price is sufficiently high that 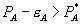 , then the bundled discount unambiguously diminishes consumer surplus and total surplus. This qualification does not affect the positive inference to be made when
, then the bundled discount unambiguously diminishes consumer surplus and total surplus. This qualification does not affect the positive inference to be made when 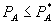 .
.
- Two Firms in the Competitive Market
So far, we have assumed that the non-monopoly market is perfectly competitive. This assumption ensured that the equilibrium prices of firm 1’s market B rivals are not affected by firm 1’s pricing strategy. Nothing changes if there is only one market B rival, provided that the B products are homogeneous and firms can set prices for B-only customers that differ from the bundle price for B.[24] The equilibrium in such cases has firm 1 setting loyalty program prices in a manner that makes the consumer indifferent between accepting the program and purchasing only B at cost, and firm 2 (the sole market B rival) setting price at marginal cost.
The duopoly results change if the firms cannot distinguish consumers that purchase A and B from those that purchase only B, or if the firms cannot prevent resale. Here, we briefly discuss how the analysis changes for this version of our first model, and examine it more deeply in a differentiated products setting in Section VII. With the assumption of homogenous goods, both firms price B at marginal cost in equilibrium absent a loyalty discount program. Introducing a bundled loyalty discount can only cause firm 1’s price of B to rise, and firm 2 may respond optimally by increasing its price. In such instances, a test in the spirit of the above is still useful. If the standalone price of A under bundling is higher than the pre-bundling monopoly price of A, then Theorem 2 implies that consumer surplus falls, even if firm 2 prices at marginal cost. To the extent that firm 2 raises its price, that conclusion is reinforced. On the other hand, if the standalone price is not greater than the pre-bundling monopoly price, we can no longer conclude that consumer surplus has declined.
- Effects on Entry and Exit
The result of firm 1’s introduction of bundled rebates has, from one perspective, a dramatic impact on firm 2: rival firms are foreclosed from serving consumers who buy both A and B. Nevertheless, the model’s assumptions imply much less stark effects in the long term. Given the assumption of perfect competition and constant marginal costs in market B, firms enter only when they have no fixed costs. To the extent that there are consumers who buy only in market B, rival firms still operate in the B market and earn normal profit. Thus for this model, bundled rebates have no additional adverse impact on competition given the potential for entry.
In fact, as discussed above, if the B market is a duopoly prior to the introduction of bundled rebates, and firms cannot distinguish A-and-B consumers from B-only consumers, then the use of bundled rebates increases profits not only for firm 1 but also for its rival. Taking this one step further, suppose that firm 1 initially has a monopoly in markets A and B, and faces a potential entrant in market B. Absent bundling, the prospect of intense competition deters entry whenever the potential entrant has positive entry costs. If firm 1 uses bundled rebates, however, the potential entrant will earn positive operating profit and thus enters when it has sufficiently small entry costs. Thus, while bundled rebates foreclose an entrant from part of the market, such a pricing strategy may induce entry by increasing the profits available to the potential entrant.
V. SMITHKLINE RECONSIDERED
An example of how our test can be applied is provided by SmithKline.[25] Lilly was the sole U.S. supplier of the cephalosporin family of antibiotics, introducing it in 1964 under the brand name Keflin. Subsequently, Lilly introduced three other cephalosporins, under the brand names Keflex, Loridine and Kafocin. Lilly had U.S. patents and exclusive rights for each of these drugs, and was the sole U.S. supplier of cephalosporins until October 1973. At that time, SmithKline entered the cephalosporin market with a drug called Ancef, obtained from a U.S. patent owner under a non-exclusive license. About a month later, Lilly introduced Kefzol, an antibiotic generically equivalent (and thus a direct competitor) to Ancef. To show how our test can be applied, we assume that Ancef and Kefzol are perfect substitutes.
Prior to entry by SmithKline, Lilly had offered volume-related rebates, as part of a Cephalosporin Savings Plan (CSP). In the latter half of 1974, Lilly examined ways to combat SmithKline, and on April 1, 1975, it introduced a Revised CSP that reduced the discount to hospitals by about 3%. At the same time, the new pricing plan gave an additional 3% rebate on a hospital’s total cephalosporin purchases provided the hospital bought certain minimum quantities, specific to each hospital, for any three of Lilly’s five cephalosporin drugs.[26]
From this discussion, the main elements of SmithKline roughly coincide with the assumptions of our model. Lilly had monopoly cephalosporin products in the Revised CSP bundle and offered a discount on the bundle. Lilly’s Kefzol and SmithKline’s Ancef were generically equivalent and, we assume, perfectly homogeneous.[27]
The Court calculated return on sales for Ancef assuming that SmithKline matched Lilly’s bundled rebates. Assuming that SmithKline produced Ancef as efficiently as Lilly made Kefzol, the Court found that SmithKline could not match Lilly’s bundled rebates without incurring losses.[28] That is, an equally efficient competitor of Kefzol (or Ancef) could not have been profitable against the Revised CSP. The Court found that Lilly had willfully maintained monopoly power under Section 2 of the Sherman Act, but found that Lilly’s pricing practices did not constitute tying, under Section 1. Thus, the Court used the Ortho test as a “bright line” test to determine whether or not Lilly’s rebates were anticompetitive.
Based on our analysis, Lilly’s bundled prices probably reduced consumer surplus and total surplus. Because the 3% loyalty discount on Lilly’s bundle was cancelled out by the roughly 3% reduction in volume-related rebates, a customer that bought the same quantity of the Lilly monopoly products under the Revised CSP as under the original CSP would have paid the same price either way. In our terminology, letting A refer to Lilly’s monopoly goods, 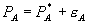 , where
, where 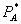 is the monopoly price prior to the Revised CSP. In other words, the standalone prices of Lilly’s monopoly goods rose under the Revised CSP and the discounted price with the loyalty rebates was approximately the same as under the original CSP. By the argument in the previous section, even if the price of Ancef rose due to Lilly’s bundling, we can conclude that the Lilly pricing strategy likely reduced consumer surplus. Furthermore, since there was no change in the price paid for the monopoly products, and the price paid for Kefzol rose, we can also conclude that total surplus declined. The Revised CSP would have the desired effect of lowering SmithKline’s sales of Ancef and preserving profits on Lilly’s cephalosporins even if the price for Kefzol were somewhat above that for Ancef.[29]
is the monopoly price prior to the Revised CSP. In other words, the standalone prices of Lilly’s monopoly goods rose under the Revised CSP and the discounted price with the loyalty rebates was approximately the same as under the original CSP. By the argument in the previous section, even if the price of Ancef rose due to Lilly’s bundling, we can conclude that the Lilly pricing strategy likely reduced consumer surplus. Furthermore, since there was no change in the price paid for the monopoly products, and the price paid for Kefzol rose, we can also conclude that total surplus declined. The Revised CSP would have the desired effect of lowering SmithKline’s sales of Ancef and preserving profits on Lilly’s cephalosporins even if the price for Kefzol were somewhat above that for Ancef.[29]
Even though the SmithKline decision was correct, our analysis suggests that its reasoning could have yielded a perverse welfare result. When the SmithKline court based its conclusion on the negative margin calculation for an equally efficient supplier of Kefzol (or Ancef), it employed the Ortho test. The Court correctly concluded that the Revised CSP foreclosed SmithKline. However, if the Revised CSP did not include higher standalone prices for the monopoly products, consumer surplus and total surplus would not have fallen (Theorem 1), yet an equally efficient competitor would have been foreclosed. Thus, the SmithKline reasoning can generate incorrect inferences about the welfare effects of bundled rebates.[30]
VI. BUNDLED DISCOUNTS AND NONLINEAR PRICES
We assumed above that positive consumer surplus exists in market A at the monopoly price. We deferred discussion of two-part tariffs and other types of nonlinear prices, partly on grounds of convenience. In some cases, two part tariffs may allow the monopolist to extract consumer surplus in market 1 completely. However, total surplus extraction is unlikely to be feasible in most cases.[31] Consistent with this is the fact that bundled discounts are often used without an entry fee, e.g. the SmithKline case discussed above. In this section we demonstrate that optimal nonlinear prices often leave positive expected consumer surplus, and that linking markets via a loyalty discount program enhances profits, even when a monopolist otherwise can offer separate nonlinear prices for each good.
Suppose that a consumer’s demand curve depends on a binary random variable, which can be “low” (L) or “high” (H) with equal probability. Let  denote demand for good i in state s, and assume that
denote demand for good i in state s, and assume that 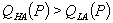 and
and 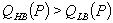 whenever demand is positive. When A and B are priced independently, competition in B makes nonlinear pricing infeasible: in equilibrium both firms price B at marginal cost and charge no entry fee.
whenever demand is positive. When A and B are priced independently, competition in B makes nonlinear pricing infeasible: in equilibrium both firms price B at marginal cost and charge no entry fee.
In market A, however, firm 1 has monopoly power and can design nonlinear prices that discriminate between the two consumer types, subject to incentive-compatibility (IC) and individual rationality (IR) constraints. For intuitive appeal, think of nonlinear prices as sets of optional two-part tariffs. Let  denote the consumer surplus of a type i consumer in market k who faces a two-part tariff with entry fee E and usage charge P. The consumer knows the realized state of nature at the time of contracting, but firm 1 does not.
denote the consumer surplus of a type i consumer in market k who faces a two-part tariff with entry fee E and usage charge P. The consumer knows the realized state of nature at the time of contracting, but firm 1 does not.
Firm 1 sets the two-part tariffs for A in order to:
 (4)
(4)
subject to:
 (IC)
(IC)
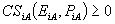 (IR)
(IR)
where 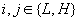 . Familiar manipulation generates the following nonlinear prices:
. Familiar manipulation generates the following nonlinear prices:
 (5)
(5)
 (6)
(6)
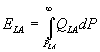 (7)
(7)
 (8)
(8)
Note that ex ante expected consumer surplus in A is positive, so there is an opportunity to increase profit by linking the two markets.
How would bundling work in this setting? Define the standalone price as the two-part tariff  , where
, where  can be made as large as desired. Thus, the consumer can purchase B at
can be made as large as desired. Thus, the consumer can purchase B at  and pay
and pay 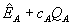 for A, if that consumer buys B from a rival of firm 1. Firm 1 offers consumers the choice of two pricing plans
for A, if that consumer buys B from a rival of firm 1. Firm 1 offers consumers the choice of two pricing plans  and
and 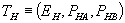 , or the outside option of purchasing A at the standalone price. For notational simplicity, define
, or the outside option of purchasing A at the standalone price. For notational simplicity, define
 .
.
A type L consumer enjoys surplus of  when it selects
when it selects 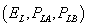 .
.
Firm 1 sets  and
and 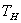 to maximize expected profits, subject to two incentive compatibility constraints (IC) and two individual rationality constraints (IR).
to maximize expected profits, subject to two incentive compatibility constraints (IC) and two individual rationality constraints (IR).
 (9)
(9)
subject to:
 (IC')
(IC')
 (IR')
(IR')
for  .
.
The right hand side of the individual rationality constraints sums the consumer surplus achieved by purchasing A at the standalone price (or foregoing A altogether) and the consumer surplus generated by buying B from a rival of firm 1. Observe that the standalone price  appears only on the right hand side of the individual rationality constraints. At a solution,
appears only on the right hand side of the individual rationality constraints. At a solution, 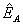 is set to weakly exceed
is set to weakly exceed 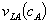 , just as the linear pricing case where the optimal standalone price
, just as the linear pricing case where the optimal standalone price  was set at least as large as the choke price
was set at least as large as the choke price  . Diminishing the outside option in this fashion relaxes the individual rationality constraints as much as possible. In equilibrium, consumers always satisfy a discount plan instead of purchasing A at
. Diminishing the outside option in this fashion relaxes the individual rationality constraints as much as possible. In equilibrium, consumers always satisfy a discount plan instead of purchasing A at 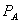 .
.
In a separating solution, 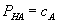 ,
,  , and
, and 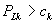 ,
,  .[32] The entry fees
.[32] The entry fees  and
and 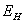 extract consumer surplus fully from type L and make type H indifferent between
extract consumer surplus fully from type L and make type H indifferent between  and
and  . Thus, the gain to firm 1 from offering a bundled loyalty discount is that second-degree price discrimination in market B now becomes feasible. Note also that expected consumer surplus remains positive. If type H’s IR' constraint does not bind, then the nonlinear prices in markets A and B are the ones that separate monopolists would set in each market. This is the nonlinear pricing version of Theorem 2.i, implying that consumer surplus and total surplus decline.
. Thus, the gain to firm 1 from offering a bundled loyalty discount is that second-degree price discrimination in market B now becomes feasible. Note also that expected consumer surplus remains positive. If type H’s IR' constraint does not bind, then the nonlinear prices in markets A and B are the ones that separate monopolists would set in each market. This is the nonlinear pricing version of Theorem 2.i, implying that consumer surplus and total surplus decline.
Since the optimal unbundled prices in (5) – (8) are a feasible outcome of the bundling problem, the monopolist earns higher profits by bundling than by using optimal unbundled two-part tariffs, given the ex ante information constraint. In terms of an upper bound on profits, from (IR') consumer surplus for each type must be at least as large as would be obtained by buying only product B at marginal cost. This implies that the bundled profits cannot exceed the entire surplus from each type in market A. Thus, the gain to bundling is at most the difference between consumer surplus in the A market at marginal cost pricing and the ex ante unbundled monopoly profits in the A market. This result formally establishes the intuition that the gains to bundled loyalty discounts are limited to what could be gained by improved nonlinear pricing in the monopoly market. This discussion has demonstrated that whether prices are linear or nonlinear, bundling can improve profits by expanding the scope for nonlinear pricing into market B.
VII. MODEL 2: IMPERFECT COMPETITION IN THE LINKED MARKET
The clean-cut nature of our welfare results thus far has depended on the assumption that market B features homogeneous goods. In this section, we relax this assumption and suppose that market B is served by duopolists that compete in a differentiated product environment. As we will show, the equivalence between tying and bundled rebates evaporates in this setting as bundled rebates take on additional facets of price discrimination.
Consumer preferences for B are uniformly distributed on the unit interval. Firm 1 is located at zero and firm 2 at one. For firm i’s product, a consumer experiences a disutility k per unit of distance between the consumer’s ideal point and firm i’s location. Denote by 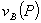 consumer surplus in the market for B gross of this cost, k. Hence, if a particular consumer’s tastes are given by
consumer surplus in the market for B gross of this cost, k. Hence, if a particular consumer’s tastes are given by  , net consumer surplus from buying B from firm 1 at price
, net consumer surplus from buying B from firm 1 at price 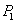 is
is 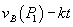 , while net consumer surplus from buying B from firm 2 at price
, while net consumer surplus from buying B from firm 2 at price 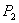 is
is 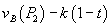 . Consumers with t values near zero prefer firm 1 while those with t near 1 prefer firm 2.
. Consumers with t values near zero prefer firm 1 while those with t near 1 prefer firm 2.
Of the unit population of consumers in the B market, a fixed fraction  uniformly distributed on the unit interval, also consume A. Thus, some A consumers prefer to buy B from firm 1 and others prefer to buy B from firm 2. As we show below, not all A consumers will buy B from firm 1 in order to obtain a discount on A. Some A-and-B consumers prefer firm 2’s product so strongly that they will pay the (higher) standalone price for A. We assume that all A consumers buy B, either from firm 1 or from firm 2. In effect, there are two consumer segments:
uniformly distributed on the unit interval, also consume A. Thus, some A consumers prefer to buy B from firm 1 and others prefer to buy B from firm 2. As we show below, not all A consumers will buy B from firm 1 in order to obtain a discount on A. Some A-and-B consumers prefer firm 2’s product so strongly that they will pay the (higher) standalone price for A. We assume that all A consumers buy B, either from firm 1 or from firm 2. In effect, there are two consumer segments:  that have positive utility for both A and B, and
that have positive utility for both A and B, and  that have positive utility only for B.
that have positive utility only for B.
As before, we denote the price of A in the bundle by 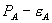 and the standalone price by
and the standalone price by 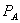 . Firm 1’s price for B is
. Firm 1’s price for B is  . Initially, we assume that firm 1 cannot charge a different price for B to bundle customers than to non-bundle customers due to arbitrage possibilities, or because firm 1 cannot prevent bundle customers from emulating non-bundle customers in the B market (perhaps by operating a separate division). As it is not in firm 1’s interests to charge a lower price for both A and B to bundled customers, firm 1 charges
. Initially, we assume that firm 1 cannot charge a different price for B to bundle customers than to non-bundle customers due to arbitrage possibilities, or because firm 1 cannot prevent bundle customers from emulating non-bundle customers in the B market (perhaps by operating a separate division). As it is not in firm 1’s interests to charge a lower price for both A and B to bundled customers, firm 1 charges 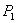 to both types of customers. Later we discuss what happens if this assumption is relaxed so that firm 1 charges different B prices to bundle and non-bundle customers. Firm 2’s uniform price for B is
to both types of customers. Later we discuss what happens if this assumption is relaxed so that firm 1 charges different B prices to bundle and non-bundle customers. Firm 2’s uniform price for B is  .
.
- Pre-Bundling
Prior to bundling, firm 1 charges the monopoly price of A,  , and competes with firm 2 in the market for B. Firm 1’s share of market B is given by
, and competes with firm 2 in the market for B. Firm 1’s share of market B is given by
 , (10)
, (10)
and firm 1’s profit is
 . (11)
. (11)
Firm 2’s profit is
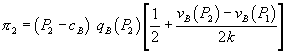 . (12)
. (12)
Note from (11) and (12) that prior to bundling, prices in B are set without regard to market A, and that firm 1’s optimal price of A does not depend on the prices for B. Therefore, in equilibrium, firm 1 charges the monopoly price for A, and both firms set the Hotelling prices in B, that is if  solves
solves 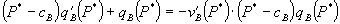 then
then  .
.
- Bundled loyalty discounts
With bundled pricing, the A and B markets interact. First, consider firm 1’s share of consumers who buy A and B. Denoting this share by  , it is given by the expression:
, it is given by the expression:
 . (13)
. (13)
Of the population of B consumers that never purchase A, firm 1’s share,  , is given by the same expression as prior to bundling:
, is given by the same expression as prior to bundling:
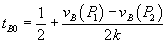 (14)
(14)
Thus, firm 1 serves  consumers that have positive utility for both A and B and
consumers that have positive utility for both A and B and 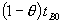 consumers who demand only B.
consumers who demand only B.
Given this notation, there are 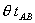 consumers that buy A and B at the bundled prices
consumers that buy A and B at the bundled prices 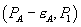 from firm 1. The mass of consumers who buy B from firm 2 and pay the standalone price for A is given by
from firm 1. The mass of consumers who buy B from firm 2 and pay the standalone price for A is given by  . Of the 1 – θ B-only consumers,
. Of the 1 – θ B-only consumers,  buy B from firm 1 and
buy B from firm 1 and  from firm 2.
from firm 2.
With these definitions, firm 1’s profit when it offers a bundled discount program is
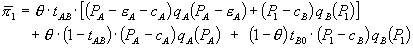 (15)
(15)
Firm 2’s profit when firm 1 bundles is
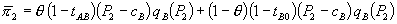 (16)
(16)
As a preliminary matter, note that the standalone price of A plays a different role with bundling than it did in Model 1. In Model 1, the only function of the standalone price is to induce consumers of A and B to buy solely via the discount program. This explains the equivalence of bundled discounts and tying in Model 1. 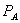 plays a similar role in Model 2, but it is also a price at which some sales may occur, to A consumers who have a strong preference for firm 2 in the B market. If
plays a similar role in Model 2, but it is also a price at which some sales may occur, to A consumers who have a strong preference for firm 2 in the B market. If  is set to make
is set to make 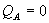 outside the bundle, some consumers may still buy B from firm 2. Hence, firm 1 does better by setting
outside the bundle, some consumers may still buy B from firm 2. Hence, firm 1 does better by setting  low enough that it can profit from selling A to consumers with strong preferences for firm 2 (t close to 1).
low enough that it can profit from selling A to consumers with strong preferences for firm 2 (t close to 1).
Comparing  to
to  , intuition suggests that for bundled discounts to be profitable, the program price of B must be higher than the price of B when there is no bundling. Firm 2’s incentives are changed, however. Instead of just competing for the
, intuition suggests that for bundled discounts to be profitable, the program price of B must be higher than the price of B when there is no bundling. Firm 2’s incentives are changed, however. Instead of just competing for the 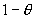 B-only consumers, firm 2 can also attract some A-and-B consumers away from the bundle. By setting
B-only consumers, firm 2 can also attract some A-and-B consumers away from the bundle. By setting 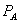 high enough, firm 1 takes from firm 2 customers that preferred firm 2 to firm 1 prior to bundling, but with bundling switch to firm 1 in order to avoid paying a high standalone price for A. Firm 2 may lower its price to compete against such a strategy.
high enough, firm 1 takes from firm 2 customers that preferred firm 2 to firm 1 prior to bundling, but with bundling switch to firm 1 in order to avoid paying a high standalone price for A. Firm 2 may lower its price to compete against such a strategy.
Letting 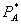 denote the monopoly profit-maximizing price for A,
denote the monopoly profit-maximizing price for A, 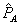 the choke price for A,
the choke price for A,  the standalone price of A with bundling, and
the standalone price of A with bundling, and  the discounted bundle price for A, we have the following partial characterization of equilibrium pricing.
the discounted bundle price for A, we have the following partial characterization of equilibrium pricing.
Theorem 3.
(1) Nash equilibrium pricing involves bundling.
(2) 
Proof. See Appendix.
From Theorem 3, the standalone price  must exceed the bundle price of A, but unlike in Model 1, it is not set to induce zero consumption. This is because firm 1 realizes that some A consumers have such a strong preference for firm 2 that it is not worth lowering
must exceed the bundle price of A, but unlike in Model 1, it is not set to induce zero consumption. This is because firm 1 realizes that some A consumers have such a strong preference for firm 2 that it is not worth lowering  in order to induce them to buy the bundle. Realizing that consumers located close to firm 2 will buy B from firm 2, firm 1 can still earn profit from such consumers by selling them A at a standalone price set between the monopoly price and the choke price. The result implies that bundled discounts are not equivalent to tie-in sales, as they were in Model 1. The standalone price acts not only to induce consumers to choose the bundle, but is part of a price discrimination device for a population of A consumers with heterogeneous tastes for B. A-and-B consumers with a preference for firm 1 in the B market purchase A at price
in order to induce them to buy the bundle. Realizing that consumers located close to firm 2 will buy B from firm 2, firm 1 can still earn profit from such consumers by selling them A at a standalone price set between the monopoly price and the choke price. The result implies that bundled discounts are not equivalent to tie-in sales, as they were in Model 1. The standalone price acts not only to induce consumers to choose the bundle, but is part of a price discrimination device for a population of A consumers with heterogeneous tastes for B. A-and-B consumers with a preference for firm 1 in the B market purchase A at price 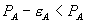 , while consumers who strongly prefer firm 2 pay
, while consumers who strongly prefer firm 2 pay 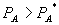 for A.
for A.
We have no general results that compare the equilibrium prices of B in the bundling regime to the pre-bundling price of B. We gain some insight by treating the standalone and bundle prices of A as exogenous variables and examine their effect on the equilibrium levels of  and
and 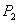 in the B market.
in the B market.
To do this, it is convenient to simplify. Let  and suppose that consumers have unit demands for B with reservation utility v . From the standpoint of firms 1 and 2, v is a random variable with distribution
and suppose that consumers have unit demands for B with reservation utility v . From the standpoint of firms 1 and 2, v is a random variable with distribution 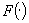 . The per capita demand function
. The per capita demand function 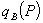 can be interpreted as
can be interpreted as  .
.
To begin, set  and
and  so that the standalone price and the bundle price equal the monopoly price
so that the standalone price and the bundle price equal the monopoly price 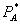 . At
. At  , the market boundary is
, the market boundary is  which is simply the market boundary under independent pricing. Hence, when
which is simply the market boundary under independent pricing. Hence, when 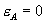 , the equilibrium levels of
, the equilibrium levels of 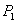 and
and  are the no-bundling levels. Standard comparative statics at
are the no-bundling levels. Standard comparative statics at 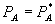 and
and  establish that
establish that
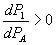 ,
, 

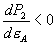 . (17)
. (17)
Thus, suppose that a “small” bundled discount  is given by raising
is given by raising  slightly above
slightly above  and lowering the bundle price slightly below
and lowering the bundle price slightly below  . Starting with
. Starting with  and
and  at their no-bundling equilibrium levels, offering the small bundled discount raises the equilibrium level of
at their no-bundling equilibrium levels, offering the small bundled discount raises the equilibrium level of  and lowers
and lowers  . The intuition for these results is what we conjectured above: firm 1 raises
. The intuition for these results is what we conjectured above: firm 1 raises  to generate incremental profit from bundling and firm 2 lowers
to generate incremental profit from bundling and firm 2 lowers 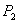 to attract A-and-B consumers that prefer its brand of B.
to attract A-and-B consumers that prefer its brand of B.
This approach is limited because the bundle and standalone prices of A are not optimal. To explore further, we assume specific linear demand curves and study simulations of the Nash equilibria of the pricing game with bundling: firm 1 chooses 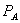 ,
, 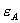 , and
, and 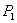 , and firm 2 chooses
, and firm 2 chooses 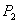 . Table One fixes the differentiation parameter k and focuses on how θ, the proportion of A-andÂÂ-B consumers, affects equilibrium pricing.[33] When there is no bundling, changes in
. Table One fixes the differentiation parameter k and focuses on how θ, the proportion of A-andÂÂ-B consumers, affects equilibrium pricing.[33] When there is no bundling, changes in  do not alter the equilibrium values of
do not alter the equilibrium values of  ,
,  , and
, and  . In contrast,
. In contrast, 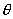 affects all prices when bundled discounts are introduced. As
affects all prices when bundled discounts are introduced. As  rises, firm 1’s price of B increases, while firm 2’s price falls. At the same time, the bundle price of A and the standalone price of A both fall. The unifying intuition is that for high values of
rises, firm 1’s price of B increases, while firm 2’s price falls. At the same time, the bundle price of A and the standalone price of A both fall. The unifying intuition is that for high values of  , more A-and-B consumers prefer firm 2’s brand of B and, therefore, can be induced to forego the bundled discount. This causes firm 1 to reduce the bundle price
, more A-and-B consumers prefer firm 2’s brand of B and, therefore, can be induced to forego the bundled discount. This causes firm 1 to reduce the bundle price  and firm 2 to reduce
and firm 2 to reduce  . As
. As 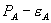 falls, the standalone price can be set closer to the monopoly price of A without reducing the incentive to choose the bundle. The bundled prices of A are all discounted substantially from the standalone prices and are much lower that the monopoly prices.
falls, the standalone price can be set closer to the monopoly price of A without reducing the incentive to choose the bundle. The bundled prices of A are all discounted substantially from the standalone prices and are much lower that the monopoly prices.
Table Two reports the welfare impacts of bundling. Aggregate net consumer surplus and producer surplus both rise in each of our simulations. Note that without bundling, firm 1’s profit increases with  , even though prices do not change. This is simply because increasing
, even though prices do not change. This is simply because increasing  expands the size of the A market.
expands the size of the A market.
A second set of simulations reported in Tables Three and Four fix 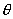 at 0.5 and vary the differentiation parameter k from 5 to 7. Increasing k makes B consumers less price-sensitive. First, as expected, prices for B rise both with and without bundling. The standalone price of A falls slightly as k increases. Intuitively, this is because when k rises, bundle customers are less likely to switch to firm 2’s brand of B whatever the prices are. Hence, the role of the standalone price shifts from enforcing choice of the bundle to maximizing profits from A-and-B consumers that prefer firm 2. On the other hand, since consumers located closer to firm 1 are now less likely to switch to
at 0.5 and vary the differentiation parameter k from 5 to 7. Increasing k makes B consumers less price-sensitive. First, as expected, prices for B rise both with and without bundling. The standalone price of A falls slightly as k increases. Intuitively, this is because when k rises, bundle customers are less likely to switch to firm 2’s brand of B whatever the prices are. Hence, the role of the standalone price shifts from enforcing choice of the bundle to maximizing profits from A-and-B consumers that prefer firm 2. On the other hand, since consumers located closer to firm 1 are now less likely to switch to 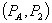 with a higher k than with a low k, the discount
with a higher k than with a low k, the discount  on the bundle price of A falls slightly, so that bundle customers pay more for A when k increases.
on the bundle price of A falls slightly, so that bundle customers pay more for A when k increases.
Table Four describes the associated welfare effects. Interestingly, they are qualitatively different from the effect of varying 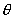 for a fixed value of k. With k = 5, consumer surplus and total surplus rise due to bundling. While producer surplus for firm 1 rises, firm 2’s surplus and overall producer surplus decline. With
for a fixed value of k. With k = 5, consumer surplus and total surplus rise due to bundling. While producer surplus for firm 1 rises, firm 2’s surplus and overall producer surplus decline. With  this pattern continues, but the rise in consumer surplus is so small and the reduction in producer surplus so large that total surplus falls. Finally, with
this pattern continues, but the rise in consumer surplus is so small and the reduction in producer surplus so large that total surplus falls. Finally, with 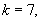 firm 1’s profits are considerably higher, but consumer surplus and firm 2’s surplus fall so much due to bundling that total surplus falls.
firm 1’s profits are considerably higher, but consumer surplus and firm 2’s surplus fall so much due to bundling that total surplus falls.
From Table Four, it is clear that the efficiency-enhancing view of bundled discounts given by Table Two is not a general result. If consumers of B are not too price sensitive (due to large k), then a bundled rebate more efficiently extracts surplus from A-and-B customers. In addition, because firm 2 is less likely to attract A-and-B customers away from firm 1’s discount program as k increases, firm 2’s equilibrium price with bundling approaches its equilibrium price in the independent pricing case.
The analysis thus far has assumed that firm 1 offers a single price in market B to both bundle and non-bundle consumers. If that assumption is relaxed (and replaced with an assumption that consumers cannot resell B purchases), simulations of the resulting equilibrium change qualitatively in only one respect. Theorem 3 still applies, so that firm 1 lowers the loyalty program price for A while raising the standalone price for A and the program price for B. Meanwhile firm 2 lowers its price for B from the non-bundling equilibrium price. The only substantive change is that firm 1 offers a price for B to non-bundled consumers that is along the Hotelling reaction curve. Given that firm 2 prices below the Hotelling equilibrium price, firm 1 responds with a price that exceeds firm 2’s price, but is less than the price in the unbundled equilibrium. In the simulations we have examined, consumers that forego the bundled rebate pay lower prices for A and B and are better off relative to the equilibrium when firm 1 charges a single price in market B, while bundled rebate participants are harmed. The general welfare effects of bundling remain ambiguous.
The ambiguous welfare results in Model 2 generally preclude using the price tests that emerged from Model 1. There is one case, however, in which a result from Model 1 carries over to the present setting. Suppose that (i) firm 1 offers separate bundle and non-bundle prices for B, (ii) as in Theorem 1, the standalone price for A remains at the unbundled monopoly price, and (iii) firm 2’s price for B falls. For this case, consumer welfare must increase relative to the equilibrium with independent pricing even though A-and-B consumers pay more for B.[34] Thus, if firm 2’s price falls and firm 1’s standalone price is no higher than it’s pre-bundling monopoly price, we have a safe harbor test, even in the Hotelling setting.
- Effects on Entry and Exit
Entry and exit effects, however, may reverse this welfare benefit. Recall that in Model 1, with homogenous goods in market B and perfect competition (or duopolists unable to distinguish A-and-B consumers from B-only consumers), the monopolist cannot use a bundled rebate to reduce entry or induce exit. While introducing a bundled rebate forecloses competitors from A-and-B consumers, it can increase the profits available to a rival in the B market. In contrast, in our differentiated products duopoly model, firm 2 earns positive profits in equilibrium which are reduced by firm 1’s use of bundled rebates. If firm 2’s profits net of fixed costs are positive in the equilibrium with independent pricing, but negative in the equilibrium with bundled rebates, then a bundled loyalty discount can induce exit. In Table 2, if  this will happen if firm 2’s fixed/entry cost is between 2.32 and 1.19. Similarly, a bundled rebate may deter entry that otherwise would occur.[35] Thus a bundled rebate scheme that enhances welfare in the short term (setting aside entry costs) will reduce welfare if the effect is to induce exit or prevent entry.
this will happen if firm 2’s fixed/entry cost is between 2.32 and 1.19. Similarly, a bundled rebate may deter entry that otherwise would occur.[35] Thus a bundled rebate scheme that enhances welfare in the short term (setting aside entry costs) will reduce welfare if the effect is to induce exit or prevent entry.
The ability of tying or bundling to act as an entry barrier is familiar from such papers as Whinston (1990), Carlton and Waldman (2002), and Nalebuff (2004a). In the first two papers, the monopolist commits to a tying strategy that changes the terms of competition in a manner that may deter potential entrants from competing head-to-head against the monopolist. In both of these papers tying benefits the monopolist only when it deters entry, and should be avoided by the monopolist if entry is inevitable. Thus, these entry deterrence benefits rely critically on the monopolist’s ability to commit to a tying strategy. The present analysis shares more in common with Nalebuff (2004a) in that bundling increases the monopolist’s profits even when the competitor is in the market, and it is the potential entrant’s anticipation that bundling is the monopolist’s optimal pricing strategy that deters it from entering.[36]
VIII. CONCLUSION
A main point of this article is that bundled rebates are not analyzed usefully based on the case law for predatory pricing. Not only are all prices typically above marginal cost, but anticompetitive effects may not require a short term profit sacrifice or a period of recoupment. Bundled rebates can generate anticompetitive effects, but they do so by confronting consumers with the choice between a collection of tied discount prices and unattractive standalone prices, all above cost.
The analogy to tying, however, does not fit bundled rebates especially well either. When the rivalrous market has homogeneous products (Model 1), equilibrium bundled rebates act as a tying arrangement (Theorem 2). When there is product differentiation in the rivalrous market (Model 2), bundled loyalty discount programs also provide a means to price discriminate between A-and-B consumers that prefer firm 1 and those that prefer firm 2. The standalone price of A has a price discrimination role quite apart from inducing consumers to choose the bundled price. This is unlike tying.
This brings us to the second main issue in this article: are there tests that distinguish good bundled rebates from bad? Although the Ortho and VAA/BA tests have their uses, the discussion above suggests that they should be used with care, if consumer welfare is a concern. In Model 1, where sellers in B produce homogenous products, there may be useful tests for consumer welfare changes based on a comparison of the monopoly price of A before and the standalone price of A after the institution of bundled rebates. Absent a reliable estimate of the unbundled monopoly price of A, they depend on there being a distinct date at which bundled discounts are introduced. For example, if B is perfectly competitive, the discounted price of A falls, and the standalone price equals the pre-bundle monopoly price, then consumer surplus and total surplus have increased, even if the bundle price of B exceeds marginal cost. Alternatively, if the firm maximizes profits and the standalone price of A exceeds the initial price of A, then we can infer that the bundled rebate reduces consumer welfare. This latter test does not apply to Model 2.
In Model 2, the pricing effects of bundling are complex and can raise or lower consumer and total welfare, even if the standalone price of A exceeds the pre-bundling monopoly price. The non-bundling firm is induced to lower its price, so in that sense a bundled loyalty discount introduced by the monopolist increases competition in the B market. On the other hand, the monopolist raises its price of B. Furthermore, as the share of A-and-B consumers increases, both the standalone and bundled prices of A fall, as competition intensifies for A-and-B consumers with a preference for firm 2. Given the potential for influencing the entry/exit decisions of competitors, there do not appear to be simple tests for whether bundling has reduced welfare as there are when the market for B is perfectly competitive.
We conclude with a discussion of what our analysis implies about when bundled loyalty discounts should be held to violate antitrust laws. In Model 1, bundled discounts work because they are a form of price discrimination among A-and-B consumers. They do not affect the price that a B-only consumer pays, and their main impact is on the consumer surplus of those who buy both A and B. Furthermore, if the monopolist can extract all surplus in the A market without bundling, then bundled rebates do not raise profits. Intuitively, bundled rebates achieve what improved nonlinear pricing would accomplish in the monopoly market. Because the bundling firm is a monopolist in A, one might argue that doing a better job of extracting surplus from a rightly earned monopoly should not be an antitrust offence. On the other hand, using a competitive market to extract monopoly rents may raise price to consumers that do not purchase the monopoly good, as well as generate deadweight losses in the competitive market that exceed the deadweight losses generated by a monopolist that does not link markets.
Model 2 has more complex implications for antitrust. Because bundled discounts can induce exit or deter entry, they have the potential to be anti-competitive by most mainstream interpretations of Section 2. Even without any exit or entry effects in Model 2, bundled discounts affect the welfare of ÂB-only consumers. However, the conditions that determine whether aggregate consumer welfare rises or falls are subtle and likely hard to measure in practice. This suggests that prospective antitrust enforcement for bundled discounts is difficult. Hence, in most cases enforcement probably should be based on actual market effects that can be traced to bundled discounts, rather than on forecasted effects.
APPENDIX
Proof of Pareto Improvement Theorem
Let 
Where 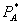 solves
solves 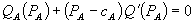 .
.
Theorem 1. Maximizing 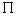 w.r.t.
w.r.t. 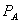 ,
, 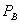 , and
, and  , at the optimum,
, at the optimum, 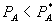 ,
, 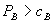 .
.
(1)  ;
;
(2)  ;
;
(3) Total welfare at 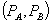 exceeds total welfare at
exceeds total welfare at  ;
;
(4) 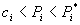 ,
,  ;
;
(5) Equally efficient competitors are foreclosed in market B.
Proof.
- The Kuhn-Tucker conditions are
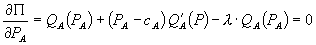 (A1)
(A1)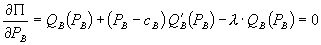 (A2)
(A2)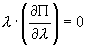 (A3)
(A3) - Suppose
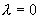 . Then (A1) and (A2) imply
. Then (A1) and (A2) imply 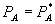 and
and 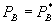 which in turn implies that
which in turn implies that  . This, however, violates the constraint, so we conclude that
. This, however, violates the constraint, so we conclude that  .
. 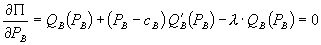 Together with (A3), this implies (1).
Together with (A3), this implies (1). - From (A1) and (A2),
 , and
, and 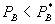 . Then (1) implies
. Then (1) implies 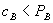 , which from (A2) means that
, which from (A2) means that  . Thus, from (A1),
. Thus, from (A1), 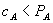 . This proves (4).
. This proves (4). - Since
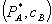 are feasible, step 3 implies (2).
are feasible, step 3 implies (2). - From (1) and (2) we have (3).
- Since (1) holds, an equally efficient competitor would have to lower prices below
 to attract customers. This proves (5).
to attract customers. This proves (5).
Proof of Corollary of 1: Linear Demand
If 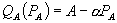 and
and 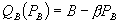 , then
, then  ,
,  ,
,  ,
,  ,
,  , and
, and 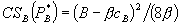 . The condition in Theorem 2 that distinguishes between the two solutions,
. The condition in Theorem 2 that distinguishes between the two solutions,  , simplifies to
, simplifies to 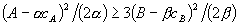 , which can be written as
, which can be written as 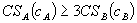 .
.
When this condition is not satisfied, the optimal  and the constraint in (3) binds. Firm 1’s maximization problem is
and the constraint in (3) binds. Firm 1’s maximization problem is
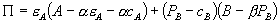 (A4)
(A4)
subject to 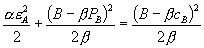
Letting  , the problem can be rewritten as
, the problem can be rewritten as
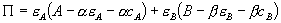 (A5)
(A5)
subject to 
Letting λ be the Lagrange multiplier for the constraint, the first order conditions are
 (A6)
(A6)
 , (A7)
, (A7)
and the solution is
 and
and  .
.
The deadweight loss at the optimal loyalty discount  can be written as
can be written as  , while the deadweight loss under independent pricing
, while the deadweight loss under independent pricing  is
is 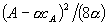 . Thus total surplus rises after firm 1 implements loyalty pricing whenever
. Thus total surplus rises after firm 1 implements loyalty pricing whenever
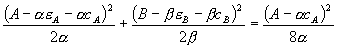 . (A8)
. (A8)
Substituting the optimal values for 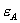 and
and 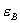 and simplifying, total surplus rises whenever
and simplifying, total surplus rises whenever
 , (A9)
, (A9)
which can be written as  .
.
Proof of Theorem 3
1. 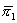 can be written as
can be written as
 (A10)
(A10)
where  is firm 1’s profit function in the B market prior to bundling.
is firm 1’s profit function in the B market prior to bundling.
From these expressions, it follows that  and
and  are feasible in the bundling problem. Hence, no bundled discount is a possible outcome.
are feasible in the bundling problem. Hence, no bundled discount is a possible outcome.
2. Differentiating with respect to 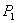 ,
,
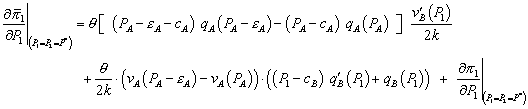 (A11)
(A11)
The last term is equal to zero at 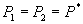 , so
, so
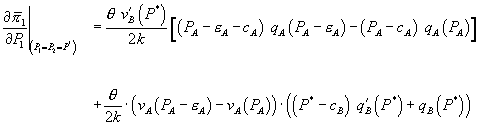 (A12)
(A12)
Since 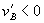 and
and 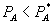 , the first right-hand side term is positive. Similarly,
, the first right-hand side term is positive. Similarly, 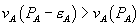 and
and 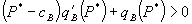 . Hence,
. Hence,
 . (A13)
. (A13)
Although the no-bundling prices are feasible for each firm, they do not satisfy the first-order conditions for firm 1 (or firm 2). This demonstrates that a no-bundling set of prices cannot be a Nash equilibrium of Model 2. This proves part (1) of the Theorem.
3. Denote 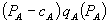 by
by  . The first order conditions for
. The first order conditions for  and
and  are:
are:
 (A14)
(A14)
 (A15)
(A15)
Note that the terms inside the brackets on the right-hand sides of (A14) and (A15) have opposite sign. Recall also that  for
for  and
and 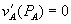 for
for 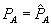 . For bundling to be incentive-compatible,
. For bundling to be incentive-compatible,  must hold. From (A14) and (A15), this requires that
must hold. From (A14) and (A15), this requires that  and
and  , because these terms cannot have the same sign. Thus,
, because these terms cannot have the same sign. Thus,  . Moreover,
. Moreover,  , so that
, so that  , which completes the proof of part (2).
, which completes the proof of part (2).
TABLE 1
EQUILIBRIUM PRICES (k = 5)
|
No Bundling |
Bundling |
||||||
|---|---|---|---|---|---|---|---|
|
? |
|
|
|
|
|
|
|
|
0 |
2.29 |
2.29 |
3.9 |
||||
|
0.2 |
2.29 |
2.29 |
3.9 |
2.30 |
4.55 |
3.45 |
2.27 |
|
0.4 |
2.29 |
2.29 |
3.9 |
2.32 |
4.44 |
3.45 |
2.25 |
|
0.6 |
2.29 |
2.29 |
3.9 |
2.35 |
4.38 |
3.41 |
2.24 |
|
0.8 |
2.29 |
2.29 |
3.9 |
2.39 |
4.34 |
3.34 |
2.22 |
|
1.0 |
2.29 |
2.29 |
3.9 |
2.48 |
4.30 |
3.20 |
2.21 |
Demands: 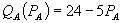 ,
, 
Marginal costs:  ,
, 
TABLE 2
SURPLUS (k = 5)
|
No Bundling |
Bundling |
Difference |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
? |
|
|
PSNB |
CSNB |
TSNB |
|
|
PSB |
CSB |
TSB |
|
|
0 |
2.32 |
2.32 |
4.63 |
30.07 |
34.70 |
||||||
|
0.2 |
3.12 |
2.32 |
5.44 |
30.48 |
35.92 |
3.14 |
1.98 |
5.13 |
32.57 |
37.70 |
1.78 |
|
0.4 |
3.94 |
2.32 |
6.25 |
30.88 |
37.13 |
4.02 |
1.76 |
5.78 |
32.66 |
38.44 |
1.31 |
|
0.6 |
4.74 |
2.32 |
7.06 |
31.29 |
38.35 |
4.93 |
1.56 |
6.49 |
32.80 |
39.28 |
0.94 |
|
0.8 |
5.56 |
2.32 |
7.87 |
31.69 |
39.56 |
5.86 |
1.37 |
7.24 |
32.92 |
40.16 |
0.59 |
|
1.0 |
6.36 |
2.32 |
8.68 |
32.10 |
40.79 |
6.90 |
1.19 |
8.09 |
32.89 |
40.98 |
0.20 |
TABLE 3
EQUILIBRIUM PRICES ( )
)
|
No Bundling |
Bundling |
||||||
|---|---|---|---|---|---|---|---|
|
k |
|
|
|
|
|
|
|
|
5 |
2.29 |
2.29 |
3.9 |
2.33 |
4.41 |
3.435 |
2.25 |
|
6 |
2.35 |
2.35 |
3.9 |
2.40 |
4.33 |
3.431 |
2.31 |
|
7 |
2.41 |
2.41 |
3.9 |
2.45 |
4.29 |
3.432 |
2.37 |
TABLE 4
SURPLUS ( )
)
|
No Bundling |
Bundling |
Difference |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
k |
|
|
PSNB |
CSNB |
TSNB |
|
|
PSB |
CSB |
TSB |
|
|
5 |
4.34 |
2.32 |
6.66 |
31.08 |
37.74 |
4.47 |
1.65 |
6.12 |
32.74 |
38.86 |
1.12 |
|
6 |
4.77 |
2.74 |
7.51 |
30.40 |
37.91 |
4.92 |
2.15 |
7.08 |
30.67 |
37.75 |
-0.17 |
|
7 |
5.16 |
3.13 |
8.29 |
29.79 |
38.08 |
5.30 |
2.57 |
7.87 |
28.86 |
36.74 |
-1.34 |
BIBLIOGRAPHY
Ahlborn C, Bailey D. Discounts, rebates and selective pricing by dominant firms: a trans-Atlantic comparison. European Competition Journal 2006;2; 101-143.
Antitrust Modernization Commission. Exclusionary conduct: refusals to deal and bundling and loyalty discounts. Hearings September 29, 2005, http :// www. amc.gov/commission_hearings/exclusionary_conduct.htm
Brennan, TJ. Competition as an entry barrier? consumer and total welfare benefits of bundling, AEI-Brookings Joint Center for Regulatory Studies Related Publication 2005 05-08.
Brown SJ, Sibley DS. The theory of public utility pricing. Cambridge University Press: Cambridge; 1986.
Burstein ML. The economics of tie-in sales. Review of Economics and Statistics 1960;42; 68-73.
Carlton D. A general analysis of exclusionary conduct and refusals to deal—why Aspen and Kodak are misguided. Antitrust Law Journal 2001;68; 659-683.
Carlton D, Waldman M. The strategic use of tying to preserve and create market power in evolving industries. RAND Journal of Economics 2002;33; 194-220.
European Commission. DG Competition discussion paper on the application of Article 82 of the Treaty to exclusionary abuses. 2005 https : // ec.europa.eu/comm/competition/antitrust/others/discpaper2005.pdf
Greenlee P, Reitman, D. Competing with loyalty discounts. EAG Discussion Paper 04-02. Washington, DC: U.S. Department of Justice, 2004.
Greenlee P, Reitman D. Distinguishing competitive and exclusionary uses of loyalty discounts. Antitrust Bulletin 2005;50; 441-464.
Hensley S. Scaled up: biggest drug firm faces generics but has an edge: its very bigness. Wall Street Journal August 23, 2004, A1.
Iyer G, Villas-Boas JM. A bargaining theory of distribution channels. Journal of Marketing Research 2003;40; 80-100.
Kadiyali V, Chintagunta P, Vilcassim N. Manufacturer-retailer channel interactions and implications for channel power: An empirical investigation of pricing in a local market. Marketing Science 2000;19; 127-148.
Kobayashi BH. The economics of loyalty discounts and antitrust law in the United States. Competition Policy International 2005;1; 115-148.
Kolay S, Shaffer G, Ordover JA. All-units discounts in retail contracts. Journal of Economics & Management Strategy 2004;13; 429-459.
Mathewson F, Winter R. Tying as a response to demand uncertainty. RAND Journal of Economics 1997;28; 566-583.
Nalebuff B. Bundling as an entry barrier. Quarterly Journal of Economics 2004a;119; 159-187.
Nalebuff B. Bundling as a way to leverage monopoly. Yale SOM Working Paper 2004b; ES-36.
Nalebuff B. Exclusionary bundling. Antitrust Bulletin 2005;50; 321-370.
Ordover JA. Willig RD. An economic definition of predation: pricing and product innovation. Yale Law Journal 1981;91; 8-53.
Parloff R. Intel’s worst nightmare. Fortune August 21, 2006, 60.
Pollack A. Johnson sues Amgen over sales practice. New York Times October 13, 2005, C2.
Rubinfeld DL. 3M’s Bundling rebates: an economic perspective. University of Chicago Law Review 2005;72; 243-264.
Sibley DS, Srinagesh P. Multiproduct nonlinear pricing with multiple taste characteristics. RAND Journal of Economics 1997;28; 684-707.
Tom WK, Balto DA, Averitt NW. Anticompetitive aspects of market-share discounts and other incentives to exclusive dealing. Antitrust Law Journal 2000;67; 615-639.
Whinston MD. Tying, foreclosure and exclusion. American Economic Review 1990;80; 837-859.
FOOTNOTES
a U.S. Department of Justice, 600 E Street NW, Suite 10000, Washington DC 20530, USA patrick.greenlee@usdoj.gov. Corresponding author. ph: 001-202-307-3745, fx: 001-202-514-5847.
b CRA International, 1201 F Street NW, Suite 700, Washington DC 20004, USA, dreitman@crai.com
c Economics Department, University of Texas at Austin, 1 University Station #C3100, Austin TX 78712, USA, dsibley@ersgroup.com
[1] 324 F.3d 141 (3rd Cir. 2003).
[2] Case T-203/01 Manufacture francaise des pneumatiques Michelin v Commission [2003] ECR II-4071.
[3] See, for example, reports on litigation involving pharmaceuticals (Hensley 2004 and Pollack 2005) and microprocessors (Parloff 2006), as well as Antitrust Modernization Commission (2005), European Commission (2005), and the commentary of Ahlborn and Bailey (2006).
[4] 427 F. Supp 1089, 1094 (E.D.PA.1976); 1976 U.S. Dist. LEXIS 12486j 1976-2 Trade Cas. (CCH), P61, 199.
[5] 920 F. Supp. 455 (1996).
[6] 257 F. 3d 256 (2001). A similar lawsuit was litigated in Europe: Case IV/D-2/34.780.
[7] One of the four counts was exclusive dealing. The jury found against LePage’s on this claim.
[8] Brooke Group Ltd. v. Brown & Williamson Tobacco Corp. 509 U.S. 209 (1993).
[9] In the context of these cases, bundling refers to a set of discount prices that are only available if the relevant products are bought largely or entirely from the dominant multi-product firm. This differs from the standard usage in economics, where bundling refers to the sale of a set number of units of various goods.
[10] Brief for the United States as Amicus Curiae, 3M Company FKA Minnesota Mining and Manufacturing Company, Petitioners, and LePage’s Incorporated, et al. On Petition for a Writ of Certiorari to the United States Court of Appeals for the Third Circuit, at 8.
[11] Their model includes small consumers that are not eligible for a loyalty program. Small consumers are always harmed by the introduction of a loyalty program, but this loss may be balanced by surplus gains to large consumers. For alternative analyses and commentary, see also Carlton (2001) and Tom et al. (2000).
[12] Consult Iyer and Villas-Boas (2003), including their discussion of the empirical study of branded tuna pricing by Kadiyali et al. (2000).
[13] See Mathewson and Winter (1997) and Brown and Sibley (1986). We address demand uncertainty in Section VI.
[14] This does not hold for less competitive settings like the differentiated products setting we study in Section VII, or when there are small consumers that cannot qualify for any loyalty discount program as in Greenlee and Reitman (2004).
[15] Mathewson and Winter (1997) establish this for a monopolist that offers a single three-part tariff to all consumer types. In Section VI, we show this for a monopolist that offers a menu of three-part tariffs to a population of two customer types. See also Sibley and Srinagesh (1997) and Iyer and Villas-Boas (2003).
[16] It would be tempting to apply this test to LePage’s. Unfortunately, the prices required are not available in the public record. For a discussion, including the approach presented here, consult Rubinfeld (2005).
[17] See Rubinfeld (2005:253).
[18] Of course, a shrewd monopolist may initially set its monopoly price artificially high in order to reach such a safe harbor after introducing a bundled loyalty discount program.
[19] This test is equivalent to determining whether pricing for A and B under the bundled rebate is “compensatory” as introduced by Ordover and Willig (1981). Ordover served as an economic expert for the plaintiff in Ortho. See also Nalebuff (2004c).
[20] The test that we propose above, though, has a similar theoretical problem: any bundled discount plan that passes it, given Theorem 1, cannot be maximizing profits.
[21] In this respect, the Ortho test once again resembles cost tests for predation.
[22] For more on how both our test and the Ortho test can be used as a safe harbor for legitimate conduct, see Greenlee and Reitman (2005).
[23] However, as mentioned above, if products are differentiated and buyers prefer a mix of products from multiple firms, then the VAA/BA incremental test can distinguish short run profit maximizing behavior from potentially exclusionary behavior. See Greenlee and Reitman (2004, 2005).
[24] An equivalent assumption would be that there are no consumers that purchase only B.
[25] Nalebuff (2005) and Kobayashi (2005) also discuss SmithKline from the standpoint of the Ortho test.
[26] See Opinion, in SmithKline, ibid Findings of Fact, paragraph 90. SmithKline argued that the total effect of the revised CSP was that “Hospitals allegedly receive approximately the same aggregate rebate under the revised CSP as that paid under the CSP.” See Opinion, p. 27.
[27] This, along with an assumption that no hospitals purchased only the Kefzol/Ancef products, enables us to apply the test. If Ancef and Kefzol were not regarded as perfect substitutes by customers, then this analysis would not apply.
[28] See Opinion, paragraph 110.
[29] As the Court noted, “So long as its price on Kefzol was equal to or not much higher than Smith-Kline’s, Lilly counted on its reputation with physicians (particularly surgeons) and the reluctance of hospitals to suffer a decline in rebates (as compared with the rebates previously received under the CSP) because of their failure to participate in the Revised CSP, as a strategy to achieve its domination (goal of 75%) of the cefazolin market.” Opinion, paragraph 101.
[30] The Third Circuit Court, which affirmed the lower court decision on appeal, came closer to the standard advocated here. The decisive factor in that opinion was that more competition, and with it lower prices, would have prevailed but for the bundled rebate scheme. 575 F. 2nd 1056 (3d Cir 1978.)
[31] See the analysis in Iyer and Villas-Boas (2003) as well as Mathewson and Winter (1997).
[32] The necessary and sufficient condition for the existence of a separating solution to the bundled nonlinear pricing problem is that there exist positive numbers εAand εB that satisfy:
 for
for 
[33] We assume demands are described by 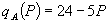 and
and  , marginal costs are
, marginal costs are 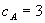 , and
, and  , and the disutility parameter is
, and the disutility parameter is  .
.
[34] Briefly, non-bundle customers clearly benefit. Bundle customers with 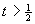 benefit because the price for B from firm 2 (their preferred provider) has fallen while the standalone price for A has not risen. The consumer at
benefit because the price for B from firm 2 (their preferred provider) has fallen while the standalone price for A has not risen. The consumer at 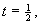 who buys the bundle and rejects an alternative that generates higher welfare than the unbundled equilibrium, must get higher welfare from the bundle. This implies that all consumers with
who buys the bundle and rejects an alternative that generates higher welfare than the unbundled equilibrium, must get higher welfare from the bundle. This implies that all consumers with  benefit from the introduction of a bundled loyalty discount. Thus welfare increases for all consumers. Without the separate market B price for unbundled customers of firm 1, the welfare effect for non-bundled customers and overall is ambiguous.
benefit from the introduction of a bundled loyalty discount. Thus welfare increases for all consumers. Without the separate market B price for unbundled customers of firm 1, the welfare effect for non-bundled customers and overall is ambiguous.
[35] Consider, for example, the results reported in Table 2. Bundled loyalty discounts deter entry (induce exit) whenever entry (fixed) costs fall between 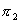 and
and  .
.
[36] Nalebuff’s environment differs from ours in that his consumers have heterogeneous unit demands for A and for B. It should be emphasized that the competitive harm here arises from firm 1 being able to maintain a monopoly. As Tables 2 and 4 illustrate, Nalebuff (2004a) describes, and Brennan (2005) explores in greater detail, bundling (or a bundled loyalty discount) often raises aggregate consumer surplus and total surplus when entry deterrence fails.

 U.S. Department
of Justice
U.S. Department
of Justice