Competition Or Collusion? Negotiating Discounts Off Posted Prices
| This document is available in two formats: this web page (for browsing content) and PDF (comparable to original document formatting). To view the PDF you will need Acrobat Reader, which may be downloaded from the Adobe site. |
| ECONOMIC ANALYSIS GROUP DISCUSSION PAPER
EAG Discussion Papers are the primary vehicle used to disseminate research from economists in the Economic Analysis Group (EAG) of the Antitrust Division. These papers are intended to inform interested individuals and institutions of EAG's research program and to stimulate comment and criticism on economic issues related to antitrust policy and regulation. The analysis and conclusions expressed herein are solely those of the authors and do not represent the views of the United States Department of Justice. Information on the EAG research program and discussion paper series may be obtained from Russell Pittman, Director of Economic Research, Economic Analysis Group, Antitrust Division, U.S. Department of Justice, BICN 10-000, Washington, DC 20530, or by e-mail at russell.pittman@usdoj.gov. Comments on specific papers may be addressed directly to the authors at the same mailing address or at their e-mail address. Recent EAG Discussion Paper titles are listed at the end of the paper. To obtain a complete list of titles or to request single copies of individual papers, please write to Janet Ficco at the above mailing address or at janet.ficco@usdoj.gov or call (202) 307-3779. Beginning with papers issued in 1999, copies of individual papers are also available from the Social Science Research Network at www.ssrn.com. Abstract Opportunities for buyers to negotiate discounts can blunt competition in the initial posting of prices. It is always an equilibrium for identical suppliers to post price at the common marginal cost. If few buyers have opportunities to bargain, this equilibrium is unique. If many buyers have bargaining opportunities, however, a second equilibrium emerges in which suppliers post the monopoly price and then negotiate discounts individually with buyers. In this equilibrium, discounted prices are above marginal cost and profits increase with concentration. Advance price announcements may help suppliers coordinate onto their preferred equilibrium of posting the monopoly price. JEL codes: C71, C78, L13, L41 1. Introduction In a number of industries, suppliers post prices and then negotiate discounts off list with individual buyers. Advance price announcements, in which suppliers publish price changes ahead of their effective dates, are also common. These pricing practices have raised concerns as possibly facilitating collusion (e.g., Grether and Plott, 1984; Borenstein, 1994; Gillespie, 1995). How do opportunities for discounting affect market pricing? Selective discounting can of course undermine collusively set prices (Stigler, 1964). Cooper (1986) and Holt and Scheffman (1987) show that most-favored-customer and best-price provisions can support high posted prices by discouraging selective discounts. Yet recent research in laboratory markets finds seemingly contrary results on the effect of discounting. Introducing opportunities for consumers to bargain for discounts often leads to market outcomes less favorable for consumers. Cason et al. (2003) find that transaction prices are higher in "haggle" markets, where suppliers post prices but consumers can negotiate discounts, than in pure posted-offer markets. Davis and Holt (1994) similarly find that when opportunities for discounting are introduced into a posted-offer market, suppliers uniformly raise their list prices, sometimes dramatically, and net prices are high. This paper develops a simple model that can explain such patterns. Identical suppliers post prices noncooperatively in an initial period, after which (some) buyers have an opportunity to approach a supplier and engage in an alternating-offers bargaining game. Posted prices affect the bargaining subgame in two ways. First, the option to buy at the lowest posted price serves as a buyer's threat-point in bargaining for a discount. The higher the lowest posted price, the worse a buyer's position in bargaining with any supplier. Second, a supplier's posted price determines the supplier's attractiveness as a bargaining partner. In particular, a high posted price makes a supplier an attractive bargaining partner, by putting the supplier in a poor bargaining position (relative to rivals posting the lowest price). This creates an incentive for suppliers to post high prices to attract buyers seeking discounts. This incentive runs counter to the more familiar incentive suppliers have to post low prices to capture sales to buyers who do not have bargaining opportunities and so buy at posted price. It is always an equilibrium for identical suppliers to post price at the common marginal cost. If the proportion of buyers with bargaining opportunities is large enough, however, a second equilibrium emerges in which all suppliers post the monopoly price and subsequently negotiate discounts with individual buyers.(1) In this equilibrium, discounted prices are strictly above marginal cost and supplier profits increase with concentration. Advance price announcements may thus help suppliers coordinate onto their preferred equilibrium of posting the monopoly price. The remainder of the paper is organized as follows. Section 2 lays out the model setting, while Section 3 describes equilibrium. Possible implications for competition policy and extensions to the model are discussed in Section 4. Section 5 concludes. 2. Economic Setting There are There is no discounting of the future. If an offer pt is accepted in any period t, the negotiating consumer receives a payoff of v - pt and the supplier receives pt - c from the given sale. If in any period the opportunity for further negotiation ends, the consumer can still buy from any supplier i at the supplier's posted price If n suppliers offer a lowest posted price To sum up: (1) the 1 - This last point is critical to the analysis. By assumption, a consumer negotiating with a supplier posting 3. Equilibrium If the lowest price posted in t = 0 is c, all consumers purchase at price c in t = 1. If the lowest posted price If a given consumer's offer is rejected and the opportunity for further negotiation ends, the consumer buys at posted price, earning a payoff of 3.1 Bargaining with a High-Posted-Price Supplier Take first the case of a consumer bargaining with a supplier that has posted a high price. In odd-numbered period t, the consumer offers a transaction price of pt, such that
where pt+1 is the optimal counter-offer the supplier would make in period t + 1 conditional on rejecting the consumer's offer of pt in t. In subgame perfect equilibrium, the counter-offer pt would be accepted by the consumer, yielding the supplier a payoff of pt+1 - c. This payoff would be realized with the probability The highest offer the consumer would accept in period t + 1 is given by
where pt+2 is the optimal counter-offer the consumer would make in t + 2 conditional on rejecting the supplier's offer of pt+1. In subgame perfect equilibrium,
That is, the parties' optimal offers and counter-offers do not change across periods. Substituting (3) into (2), the supplier's optimal offer in t + 1 can be written as
Substituting (4) into (1) and solving for pt yields the consumer's offer in t as
If a consumer were to offer the price pt given in equation (5) to a supplier that has posted a high price, the supplier would accept immediately in period t. 3.2 Bargaining with a Low-Posted-Price Supplier Now consider the case of a consumer bargaining with a supplier whose posted price is the low price
where the second set of terms on the right-hand side of equation (6) reflects the 1/n chance that the supplier would sell to the given consumer at posted price
An offer of pt given by equation (7) made to a supplier that has posted the low price 3.3 Equilibrium Posted Prices By posting a high price, a supplier puts itself in a poor bargaining position and so makes itself an attractive bargaining partner, as shown presently. Lemma 1. If suppliers were to post differing prices, buyers that have an opportunity to negotiate discounts would choose high-posted-price suppliers as bargaining partners over suppliers posting the low price Proof: From equations (6) and (7), a buyer pays a lower negotiated price by bargaining with a high-posted-price supplier than by bargaining with a supplier that has posted the low price. Q.E.D. The intuition underlying Lemma 1 is that if negotiations with a high-posted-price supplier were to break down, the supplier would lose the sale to the given buyer with certainty. In contrast, a supplier posting the low price Lemma 2. All active suppliers post the same price in equilibrium. Proof: Suppose to the contrary that differing prices are posted by suppliers making positive sales. This implies the low posted price is Lemmas 1 and 2 together indicate that the equilibrium posted price may be either very low or very high, depending on the pool of buyers with bargaining opportunities. If this pool is large, a high-posted-price equilibrium can be supported. The critical value of
Proposition 1. The following completely describes posted prices in subgame perfect equilibria of the game:
Proof: The proof of part (i) is immediate. Proof of parts (ii)-(iv) is left to the Appendix, but is sketched here. Let 3.4 Equilibrium Discounted Price If
Proposition 2. Suppose
![\[ \tilde p > c \]](/atr/public/eag/221873/61.gif) . . The discounted price Proof: Subtracting c from equation (9), the margin earned on sales to negotiating buyers can be written as
which completes the proof of part (i). For proof of part (ii), differentiate equation (10) with respect to
Finally, the discounted price decreases with N by inspection of equation (9). Q.E.D. Intuitively, increasing 4. Discussion The modeling results can be summarized as follows. Any given supplier sees an upside as well as a downside to posting a high price. Posting a price higher than rivals' posted prices loses sales to buyers that have no bargaining opportunities and so transact at posted price, but gains sales to buyers seeking discounts, by putting the supplier in a poor bargaining position. If few buyers have bargaining opportunities, the tradeoff favors posting lower prices. In this case suppliers compete fiercely in posting prices and all post price at the common marginal cost in the unique equilibrium. If many buyers have bargaining opportunities, however, the tradeoff favors posting higher prices. In this case, although it remains an equilibrium for suppliers to post price at marginal cost, a second equilibrium emerges in which suppliers post the monopoly price. In this second equilibrium, competition for sales to buyers with bargaining opportunities blunts competition in the initial posting of prices. More precisely, a perverse form of competition then takes hold, in which suppliers race to the top. The outcome of the game when suppliers post a price above marginal cost reflects a form of price discrimination. Buyers without bargaining opportunities transact at posted price, while buyers with bargaining opportunities pay a discounted price and enjoy more surplus. Surplus is then lower for every buyer and supplier profits are higher (positive) as compared with the equilibrium in which suppliers post price at marginal cost. The remainder of this section discusses further implications and possible extensions of the model. 4.1 Advance Price Announcements and Mergers By Proposition 1, there are multiple posted price equilibria when the proportion of buyers with bargaining opportunities is high, In the present modeling context, effective coordination might be limited to suppliers choosing among noncooperative equilibria of the game; it need not involve an agreement to refrain from discounting. Such limited coordination might, nevertheless, raise prices substantially above marginal cost. Let
The table below presents values of
In a duopoly, margins are 75% of the monopoly level. Margins decline with the number of competing suppliers, but remain above half of the monopoly margin even for N = 10. The table also suggests that if suppliers coordinate onto a high-posted-price equilibrium, a merger of homogeneous good suppliers could raise the equilibrium net price significantly. For example, if 4.2 Commitment Power In a narrow bargaining context, the ability to commit to an offer is advantageous. Greater commitment power typically allows the committed party to capture more of the joint surplus from trade (e.g., Schelling, 1960; Crawford, 1982; Muthoo, 1996; Kambe, 1999). In the broader context of market equilibrium, however, such commitment power is disadvantageous in the present setting. Consider the case of This suggests that suppliers in posted-offer markets may have an incentive to soften their ability to commit to posted offers. Consistent with this possibility is the observation that suppliers in posted-offer markets sometimes encourage the formation of buyer groups that strengthen the bargaining power of smaller buyers.(5) 4.3 Selective Discounts Suppliers are rather passive with respect to discounting in the model. Buyers with bargaining opportunities take the initiative in choosing bargaining partners and making discount offers. However, suppliers might also seek out buyers that have no bargaining opportunities and offer them selective discounts. Such supplier-initiated discounting could be profitable if suppliers could distinguish between buyer types well enough. Corts (1998) shows that, in an oligopoly market, third-degree price discrimination can intensify competition, lowering suppliers' profits and raising the surplus of every consumer type. A similar result holds in the present context. If selective discounting initiated by suppliers were individually profitable, a high-posted-price equilibrium could not be sustained. Let
Substituting equation (10) into expression (13), note that expression (13) is positive if
Substituting inequality (14) requires If suppliers were adept enough at identifying buyer types, selective discounting could be profitable, in which case a posted price above marginal cost could not be sustained; posting 4.4 Bargaining Opportunities Buyer bargaining opportunities have so far been treated as exogenous. Such opportunities of course depend on market characteristics. For example, the search costs facing buyers wishing to engage in serial discount negotiations may decline with the number of suppliers in the market. The ability to negotiate discounts also depends on such factors as a buyer's risk-aversion, impatience and outside options. The more these factors are associated with observable buyer characteristics, such as buyer size, the more information suppliers would tend to have on which to base selective discounts. A growing literature has explored how buyer size may affect the prices buyers obtain. One strand of this literature involves models of bilateral and multilateral bargaining in which the parties split the increment to total surplus from their reaching a deal. Papers in this vein include Horn and Wolinsky (1988), Stole and Zweibel (1996a,b), Chipty and Snyder (1999), Inderst and Wey (2003) and Raskovich (2003). These authors all find that larger buyers do not necessarily negotiate lower prices. The relationship between buyer size and price depends on the curvature of total surplus with respect to the volume of trade. If increments to total surplus diminish (grow) at the margin, a buyer's bargaining leverage falls (rises) with the size of the buyer's purchase requirements. Raskovich (2003) further shows that if a buyer is so large as to be pivotal to a supplier's entry decision, the buyer is in a worse bargaining position vis-à-vis the supplier than are smaller, non-pivotal buyers whose purchases have no effect on the supplier's decision to sink costs.(8) Experimental work by Normann et al. (2005) supports these conclusions, finding that large buyers receive discounts only in the case of increasing marginal costs (concave surplus function). 5. Concluding Remarks Opportunities for buyers to negotiate discounts can affect competition in posted-offer markets in a surprising way. If the pool of buyers with bargaining opportunities is large enough, competition to attract such buyers can lead suppliers in a "race to the top" to post a high price in equilibrium. Given that it is also (always) an equilibrium for identical suppliers to post price at common marginal cost, advance price announcements might help suppliers to coordinate onto their preferred equilibrium of posting the monopoly price. Such (limited) coordination is stable because the agreed-upon posted price is a noncooperative equilibrium. When posted price is high in the market outcome, discounting off will be pervasive and vigorous, yet negotiated prices will remain well above marginal cost. In this case, a merger of homogeneous good suppliers could result in a significant increase in net prices. Appendix Proof of Proposition 1(ii): By Lemma 2, focus on cases in which all N suppliers post a common price
given that the proportion 1 -
Substituting (A2) into (A1) and simplifying yields
If a supplier were to post a price an arbitrarily small amount below
The increment to profit from undercutting
and the sign does not depend on the precise value of
Solving (A6) for the critical value
given Proof of Proposition 1(iii): From the proof of part 1(ii),
Let
Note that the sign of
By (A6) and the definition of
the inequality being strict when
which is strictly greater than (A10) when Proof of Proposition 1(iv): From the proof of part 1(ii), References Binmore, K., Rubinstein, A., Wolinsky, A., 1986. The Nash bargaining solution in economic modeling. Rand Journal of Economics 17, 176-188. Blair, R.D., Romano, R.E., 2002. Advance price announcements and antitrust policy. International Review of Law and Economics 21, 435-452. Borenstein, S., 1994. Rapid price communication and coordination: the airline tariff publishing case. In: Kwoka, J.E., White, L.J. (Eds.), The Antitrust Revolution: Economics, Competition, and Policy, 3rd Ed., 1999. Oxford University Press, New York, pp. 310-326. Cason, T.N., Friedman, D., Milam, G.H., 2003. Bargaining versus posted price competition in customer markets. International Journal of Industrial Organization 21, 223-251. Chipty, T., Snyder, C.A., 1999. The role of firm size in bilateral bargaining: a study of the cable television industry. Review of Economics and Statistics 81, 326-340. Cooper, T.C., 1986. Most-favored customer pricing and tacit collusion. RAND Journal of Economics 17, 377-388. Corts, K.S., 1998. Third-degree price discrimination in oligopoly: all-out competition and strategic commitment. RAND Journal of Economics 29, 306-323. Crawford, V., 1982. A theory of disagreement in bargaining. Econometrica 50, 607-637. Davis, D.D., Holt, C.A., 1994. The effects of discounting opportunities in laboratory posted-offer markets. Economics Letters 44, 249-253. Gillespie, W., 1995. Cheap talk, price announcements, and collusive coordination. Economic Analysis Group Discussion Paper 95-3, U.S. Department of Justice. Grether, D.M., Plott, C.R., 1984. The effects of market practices in oligopolistic markets: an experimental examination of the ethyl case. Economic Inquiry 22, 479-528. Holt, C.A., Scheffman, D.T., 1987. Facilitating practices: the effects of advance notice and best-price policies. RAND Journal of Economics 18, 187-197. Horn, H., Wolinsky, A., 1988. Bilateral monopolies and incentive for merger. RAND Journal of Economics 19, 408-419. Kambe, S., 1999. Bargaining with imperfect commitment. Games and Economic Behavior 28, 217-237. Mathewson, F., Winter, R.A., 1997. Buyer groups. International Journal of Industrial Organization 15, 131-164. Muthoo, A., 1996. A bargaining model based on the commitment tactic. Journal of Economic Theory 69, 134-152. Normann, H.T., Ruffle, B.J., Snyder, C.M., 2005. Do buyer-size discounts depend on the curvature of the surplus function? Experimental tests of bargaining models. http://ssrn.com/abstract=422780. Inderst, R., Wey, C., 2003. Bargaining, mergers, and technology choice in bilaterally oligopolistic industries. RAND Journal of Economics 34, 1-19. Raskovich, A., 2003. Pivotal buyers and bargaining position. Journal of Industrial Economics 51, 405-426. Rubinstein, A., 1982. Perfect equilibrium in a bargaining model. Econometrica 50, 97-109. Schelling, T., 1960. The Strategy of Conflict. Harvard University Press, Cambridge, MA. Stigler, G.J., 1964. A theory of oligopoly. Journal of Political Economy 72, 44-61. Stole, L.A., Zweibel, J., 1996a. Intra-firm bargaining under non-binding contracts. Review of Economic Studies 63, 375-410. Stole, L.A., Zweibel, J., 1996b. Orgainizational design and technology choice under intrafirm bargaining. American Economic Review 86, 88-102. FOOTNOTES * Economist, Antitrust Division, U.S. Department of Justice. The views expressed are solely my own and not those of the U.S. Department of Justice. For helpful comments and suggestions, I thank Patrick Greenlee, Russ Pittman and especially two anonymous referees and the editor, Bernard Caillaud. 1. As shown below, when the pool of buyers with bargaining opportunities is large, there is also a razor's edge duopoly case for which a continuum of equilibria exists. 2. Alternatively, suppose every consumer has a "special" good, with reservation value 3. Suppliers' collective profits in posted-price equilibrium 4. Blair and Romano (2002) show that when advance price announcements resolve cost uncertainty, both profits and consumer surplus rise. 5. See Matthewson and Winter (1997) for an alternative explanation of buyer groups, in which such groups help to internalize market externalities in a tradeoff between cost and variety. 6. Here the lack of bargaining opportunities by a buyer is interpreted as the supplier having the ability to make a take-it-or-leave-it offer to the buyer. 7. Recall that 8. A supplier's binary entry decision could be viewed as a special case of the total surplus function being convex with respect to the incremental volume of reaching a deal with a pivotal buyer. |

 U.S. Department
of Justice
U.S. Department
of Justice
![\[ N \ge 2 \]](/atr/public/eag/221873/1.gif) suppliers producing a homogeneous good at the common constant marginal cost
suppliers producing a homogeneous good at the common constant marginal cost ![\[ c \ge 0 \]](/atr/public/eag/221873/2.gif) , and there is a continuum of consumers of measure one, each of whom has unit demand for the good at the common reservation value v > c. The game is played over an infinite number of periods, indexed by t. Suppliers (indexed by i) simultaneously post prices
, and there is a continuum of consumers of measure one, each of whom has unit demand for the good at the common reservation value v > c. The game is played over an infinite number of periods, indexed by t. Suppliers (indexed by i) simultaneously post prices ![\[ \bar p_t \]](/atr/public/eag/221873/4.gif) in period t = 0. At t = 1, every consumer has, with independent probability
in period t = 0. At t = 1, every consumer has, with independent probability ![\[ \theta \]](/atr/public/eag/221873/7.gif) , an opportunity to make an offer to a chosen supplier. If the chosen supplier rejects a given consumer's offer, then with probability
, an opportunity to make an offer to a chosen supplier. If the chosen supplier rejects a given consumer's offer, then with probability ![\[ v - p_t \]](/atr/public/eag/221873/13.gif) and the supplier receives
and the supplier receives ![\[ p_t - c \]](/atr/public/eag/221873/14.gif) from the given sale.
from the given sale. ![\[ \bar p_L \]](/atr/public/eag/221873/15.gif) no greater than v, a consumer buying at posted price chooses among these suppliers with equal probability 1/n. Likewise, if m suppliers post some price
no greater than v, a consumer buying at posted price chooses among these suppliers with equal probability 1/n. Likewise, if m suppliers post some price ![\[ \bar p \]](/atr/public/eag/221873/17.gif) and a consumer with an opportunity to negotiate prefers to bargain with a supplier posting \bar p, the consumer chooses a bargaining partner among these suppliers with equal probability 1/m.
and a consumer with an opportunity to negotiate prefers to bargain with a supplier posting \bar p, the consumer chooses a bargaining partner among these suppliers with equal probability 1/m. ![\[ v - \bar p_L \ge 0 \]](/atr/public/eag/221873/21.gif) . In this case, the supplier's expected payoff with regard to the given consumer depends on whether the supplier has posted
. In this case, the supplier's expected payoff with regard to the given consumer depends on whether the supplier has posted ![\[ {\textstyle{1 \over n}}\,\left( {\bar p_L - c} \right) > 0 \]](/atr/public/eag/221873/22.gif) if negotiations break down, because the consumer is assumed to buy with equal probability from among the n suppliers posting
if negotiations break down, because the consumer is assumed to buy with equal probability from among the n suppliers posting ![\[ p_t - c = \theta \,\left( {p_{t + 1} - c} \right) \]](/atr/public/eag/221873/23.gif) ,
,![\[ v - p_{t + 1} = \theta \,\left( {v - p_{t + 2} } \right) + \left( {1 - \theta } \right)\,\left( {v - \bar p_L } \right) \]](/atr/public/eag/221873/27.gif) ,
,![\[ p_{t + 1} = \theta \,p_t + \left( {1 - \theta } \right)\,\bar p_L \]](/atr/public/eag/221873/31.gif) .
. ![\[ p_t = \frac{1}{{1 + \theta }}\;\left( {\theta \,\bar p_L + c} \right) \]](/atr/public/eag/221873/32.gif) (to a high posted-price supplier).
(to a high posted-price supplier).![\[ p_t - c = \theta \,\left( {p_{t + 1} - c} \right) + \left( {1 - \theta } \right)\,\left( {{\textstyle{1 \over n}}} \right)\,\left( {\bar p_L - c} \right) \]](/atr/public/eag/221873/33.gif) .
. ![\[ p_t = \frac{1}{{1 + \theta }}\;\left[ {\theta \,\bar p_L + c + {\textstyle{1 \over n}}\,\left( {\bar p_L - c} \right)} \right] \]](/atr/public/eag/221873/34.gif) (to a low posted-price supplier).
(to a low posted-price supplier).![\[ \bar p_L \in (c,\,v) \]](/atr/public/eag/221873/35.gif) ; otherwise no high-posted-price supplier would make any sales if
; otherwise no high-posted-price supplier would make any sales if ![\[ \bar p_L = c \]](/atr/public/eag/221873/36.gif) . Also
. Also ![\[ \theta \in (0,\,1) \]](/atr/public/eag/221873/37.gif) by Lemma 1; otherwise no high-posted-price supplier would make any sales if
by Lemma 1; otherwise no high-posted-price supplier would make any sales if 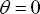 , and no low-posted-price supplier would make any sales if
, and no low-posted-price supplier would make any sales if ![\[ \theta = 1 \]](/atr/public/eag/221873/39.gif) . Now note that a supplier's unit sales depend only on the supplier's price ranking and the number of suppliers posting the same price. Consider two cases involving suppliers posting
. Now note that a supplier's unit sales depend only on the supplier's price ranking and the number of suppliers posting the same price. Consider two cases involving suppliers posting ![\[ ({1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n})\,(1 - \theta ) \]](/atr/public/eag/221873/41.gif) by Lemma 1. Any such supplier could increase unit sales discretely to 1 -
by Lemma 1. Any such supplier could increase unit sales discretely to 1 - ![\[ \theta *(N)\;\; = \;\;\frac{{\sqrt {4\,N^3 (N - 1) + 1} \;\; - \;1}}{{2\,N^2 }} \]](/atr/public/eag/221873/42.gif) .
. ![\[ \theta \in [0,\,1] \]](/atr/public/eag/221873/43.gif) and
and ![\[ \bar p = c \]](/atr/public/eag/221873/44.gif) , and
, and ![\[ \theta < \theta *(N) \]](/atr/public/eag/221873/45.gif) .
. ![\[ \theta \ge \theta *(N) \]](/atr/public/eag/221873/46.gif) and at least one of these two inequalities is strict, there is a second equilibrium in which suppliers post the monopoly price,
and at least one of these two inequalities is strict, there is a second equilibrium in which suppliers post the monopoly price, ![\[ \bar p = v \]](/atr/public/eag/221873/47.gif) , and there is no third equilibrium.
, and there is no third equilibrium. ![\[ \theta = \theta *(2) \]](/atr/public/eag/221873/49.gif) , any common posted price
, any common posted price ![\[ \bar p \in [c,\,v] \]](/atr/public/eag/221873/50.gif) is an equilibrium.
is an equilibrium.![\[ \Delta _L \]](/atr/public/eag/221873/51.gif) denote the incremental profit a supplier would earn by undercutting a common posted price
denote the incremental profit a supplier would earn by undercutting a common posted price ![\[ sign\,\left( {\Delta _L } \right)\;\, = \,\;sign\,\left( {\theta *(N) - \theta } \right) \]](/atr/public/eag/221873/52.gif) . Thus if
. Thus if ![\[ \bar p > c \]](/atr/public/eag/221873/53.gif) , and so posting
, and so posting ![\[ \Delta _H \]](/atr/public/eag/221873/54.gif) be the incremental profit a supplier would earn by raising posted price above some
be the incremental profit a supplier would earn by raising posted price above some ![\[ \Delta _H > 0 \]](/atr/public/eag/221873/55.gif) for
for ![\[ \Delta _H = \Delta _L = 0 \]](/atr/public/eag/221873/56.gif) . In this razor's edge case, any
. In this razor's edge case, any ![\[ \tilde p \]](/atr/public/eag/221873/57.gif) , can be obtained from equation (7) by setting
, can be obtained from equation (7) by setting ![\[ \bar p_L = \bar p \]](/atr/public/eag/221873/58.gif) and n = N:
and n = N: ![\[ \tilde p\;\; = \;\;\frac{1}{{1 + \theta }}\;\left[ {\theta \,\bar p + c + {\textstyle{1 \over N}}\,\left( {\bar p - c} \right)} \right] \]](/atr/public/eag/221873/60.gif) .
.![\[ \tilde p - c\;\; = \;\;\frac{{1 + N\,\theta }}{{N\,(1 + \theta )}}\;(\bar p - c)\;\; > \;\;0 \]](/atr/public/eag/221873/62.gif) ,
,![\[ \frac{\partial }{{\partial \,\theta }}\;(\tilde p - c)\;\; = \;\;\frac{{N - 1}}{{N\,(1 + \theta )^2 }}\;(\bar p - c)\;\; > \;\;0 \]](/atr/public/eag/221873/63.gif) .
.![\[ \theta *(N) \]](/atr/public/eag/221873/65.gif) above which high-posted-price equilibria are possible. Note from equation (8) that, for example,
above which high-posted-price equilibria are possible. Note from equation (8) that, for example, ![\[ \theta *(2) \approx 0.59 \]](/atr/public/eag/221873/66.gif) ,
, ![\[ \theta *(3) \approx 0.76 \]](/atr/public/eag/221873/67.gif) ,
, ![\[ \theta *(10) \approx 0.94 \]](/atr/public/eag/221873/68.gif) , and generally that
, and generally that ![\[ \theta *(N) \to 1 \]](/atr/public/eag/221873/65b.gif) as
as ![\[ N \to \infty \]](/atr/public/eag/221873/69.gif) .
. ![\[ \mu (\theta ,\,N) \]](/atr/public/eag/221873/70.gif) be the margin suppliers earn on sales at the negotiated price
be the margin suppliers earn on sales at the negotiated price ![\[ \mu (\theta ,\,N) \equiv {{(\tilde p - c)} \mathord{\left/ {\vphantom {{(\tilde p - c)} {(v - c)}}} \right. \kern-\nulldelimiterspace} {(v - c)}} \]](/atr/public/eag/221873/71.gif) . By equation (10), this equilibrium margin is
. By equation (10), this equilibrium margin is ![\[ \mu (\theta ,\,N)\;\; = \;\;\frac{{\theta \,N + 1}}{{(1 + \theta )\,N}} \]](/atr/public/eag/221873/72.gif) .
.![\[ \mu \]](/atr/public/eag/221873/73.gif) for
for ![\[ \mu (1,\,N) \]](/atr/public/eag/221873/74.gif)
![\[ v = 2\,c \]](/atr/public/eag/221873/76.gif) and
and ![\[ \bar p \]](/atr/public/eag/221873/77.gif) , so the proportion
, so the proportion ![\[ \gamma \]](/atr/public/eag/221873/78.gif) be the probability with which a supplier could correctly identify a given buyer as lacking bargaining opportunities. Note that
be the probability with which a supplier could correctly identify a given buyer as lacking bargaining opportunities. Note that ![\[ \gamma \ge 1 - \theta \]](/atr/public/eag/221873/79.gif) , the equality being strict if the supplier cannot distinguish buyer types better than a random draw. Now consider the case of
, the equality being strict if the supplier cannot distinguish buyer types better than a random draw. Now consider the case of ![\[ 1 - \gamma \]](/atr/public/eag/221873/80.gif) the supplier would err, the offer being received by a buyer with bargaining opportunities. In this case, by Lemma 1, the supplier would lose the 1/N chance of selling to the buyer at the negotiated price
the supplier would err, the offer being received by a buyer with bargaining opportunities. In this case, by Lemma 1, the supplier would lose the 1/N chance of selling to the buyer at the negotiated price ![\[ \gamma \,\left( {\frac{{N - 1}}{N}} \right)\,\left( {\bar p - c} \right)\;\; - \;\;\left( {1 - \gamma } \right)\,\left( {\frac{1}{N}} \right)\,\left( {\tilde p - c} \right) \]](/atr/public/eag/221873/81.gif) .
.![\[ \gamma \;\; > \;\;\frac{{\theta \,N + 1}}{{(1 + \theta )\,N^2 - N + 1}} \]](/atr/public/eag/221873/82.gif) .
.![\[ \gamma = 1 - \theta \]](/atr/public/eag/221873/83.gif) into (14) would imply
into (14) would imply ![\[ \theta = {\textstyle{3 \over 4}} \]](/atr/public/eag/221873/85.gif) ,
,![\[ \gamma > {\textstyle{5 \over {12}}} \]](/atr/public/eag/221873/86.gif) , whereas
, whereas ![\[ 1 - \theta = {\textstyle{1 \over 4}} \]](/atr/public/eag/221873/87.gif) .
. ![\[ \pi (\bar p)\;\; = \;\;\frac{1}{N}\left\{ {\,\left[ {(1 - \theta )\,\bar p + \theta \,\tilde p} \right] - c\,} \right\} \]](/atr/public/eag/221873/88.gif) ,
,![\[ \tilde p\;\; = \;\;\frac{1}{{1 + \theta }}\;\left[ {\theta \,\bar p + c + {\textstyle{1 \over N}}\,\left( {\bar p - c} \right)} \right] \]](/atr/public/eag/221873/89.gif) .
.![\[ \pi (\bar p)\;\; = \;\;\frac{{N + \theta }}{{N^2 (1 + \theta )}}\;(\bar p - c) \]](/atr/public/eag/221873/90.gif) .
.![\[ \pi _L (\bar p)\;\; = \;\;(1 - \theta )\,(\bar p - c) \]](/atr/public/eag/221873/91.gif) .
. ![\[ \Delta _L \equiv \pi _L (\bar p) - \pi (\bar p) \]](/atr/public/eag/221873/92.gif) . Subtracting (A3) from (A4) to obtain
. Subtracting (A3) from (A4) to obtain ![\[ sign\,\left( {\Delta _L } \right)\;\; = \;\;sign\,\left( {1 - \theta - \frac{{N + \theta }}{{N^2 (1 + \theta )}}} \right) \]](/atr/public/eag/221873/93.gif) .
.![\[ N^2 \,\theta ^2 + \theta - N\,(N - 1)\;\; = \;\;0 \]](/atr/public/eag/221873/94.gif) .
.![\[ \frac{{\partial \,\Delta _L }}{{\partial \,\theta }}\;\; = \;\;\frac{{N - 1 - N^2 \,(1 + \theta )^2 }}{{N^2 \,(1 + \theta )^2 }}\;(\bar p - c)\;\; < \;\;0 \]](/atr/public/eag/221873/95.gif) ,
,![\[ \Delta _L > 0 \]](/atr/public/eag/221873/96.gif) . In this case no
. In this case no ![\[ \theta > \theta *(N) \]](/atr/public/eag/221873/97.gif) implies
implies ![\[ \Delta _L < 0 \]](/atr/public/eag/221873/98.gif) . Thus no supplier could gain by undercutting a common posted price
. Thus no supplier could gain by undercutting a common posted price ![\[ \pi _H (\bar p)\;\; = \;\;\theta \,(\tilde p - c) \]](/atr/public/eag/221873/99.gif) .
.![\[ \Delta _H \equiv \pi _H (\bar p) - \pi (\bar p) \]](/atr/public/eag/221873/100.gif) . By (A2), (A3) and (A8),
. By (A2), (A3) and (A8), ![\[ \Delta _H \;\; = \;\;\frac{{N^2 \,\theta ^2 + (N - 1)\,\theta - N}}{{N^2 \,(1 + \theta )}}\;(\bar p - c) \]](/atr/public/eag/221873/101.gif) .
.![\[ N^2 \,\theta ^2 + (N - 1)\,\theta - N \]](/atr/public/eag/221873/102.gif) .
.![\[ N^2 \,\theta ^2 \ge N\,(N - 1) - \theta \]](/atr/public/eag/221873/103.gif) ,
,![\[ (N - 2)\,(N + \theta ) \]](/atr/public/eag/221873/104.gif) ,
,![\[ \theta = \theta *(N) \]](/atr/public/eag/221873/106.gif) implies
implies ![\[ \Delta _L = 0 \]](/atr/public/eag/221873/107.gif) for any
for any ![\[ \Delta _H = 0 \]](/atr/public/eag/221873/108.gif) for any
for any ![\[ v + \delta \]](/atr/public/eag/221873/109.gif) , where
, where ![\[ \delta > 0 \]](/atr/public/eag/221873/110.gif) but small. Each good has 1/N chance of being the special one for any given consumer. The identity of the special good is revealed after bargaining typically concludes, say at the close of t = 1. With
but small. Each good has 1/N chance of being the special one for any given consumer. The identity of the special good is revealed after bargaining typically concludes, say at the close of t = 1. With ![\[ \delta \]](/atr/public/eag/221873/111.gif) small, a consumer will buy at the negotiated discount even if another supplier is revealed to offer the special good. Nor is delay to resolve the uncertainty worthwhile given the probability of breakdown. In this setting, the posited threat is not credible: the supplier with whom negotiations have broken down may turn out to have the consumer's special good.
small, a consumer will buy at the negotiated discount even if another supplier is revealed to offer the special good. Nor is delay to resolve the uncertainty worthwhile given the probability of breakdown. In this setting, the posited threat is not credible: the supplier with whom negotiations have broken down may turn out to have the consumer's special good. ![\[ (1 - \theta )\,\bar p + \theta \,\tilde p \]](/atr/public/eag/221873/112.gif) and decrease with
and decrease with