The Need To Measure The Effect Of Merger Policy And How To Do It
| This document is available in two formats: this web page (for browsing content) and PDF (comparable to original document formatting). To view the PDF you will need Acrobat Reader, which may be downloaded from the Adobe site. |
| ECONOMIC ANALYSIS GROUP
EAG Discussion Papers are the primary vehicle used to disseminate research from economists in the Economic Analysis Group (EAG) of the Antitrust Division. These papers are intended to inform interested individuals and institutions of EAG's research program and to stimulate comment and criticism on economic issues related to antitrust policy and regulation. The analysis and conclusions expressed herein are solely those of the authors and do not represent the views of the United States Department of Justice. Information on the EAG research program and discussion paper series may be obtained from Russell Pittman, Director of Economic Research, Economic Analysis Group, Antitrust Division, U.S. Department of Justice, BICN 10-000, Washington, DC 20530, or by e-mail at russell.pittman@usdoj.gov. Comments on specific papers may be addressed directly to the authors at the same mailing address or at their e-mail address. Recent EAG Discussion Paper titles are listed at the end of this paper. To obtain a complete list of titles or to request single copies of individual papers, please write to Janet Ficco at the above mailing address or at janet.ficco@usdoj.gov or call (202) 307-3779. Beginning with papers issued in 1999, copies of individual papers are also available from the Social Science Research Network at www.ssrn.com. Abstract In this article, I explain the inadequacy of our current state of knowledge regarding the effectiveness of antitrust policy towards mergers. I then discuss the types of data that one must collect in order to be able to perform an analysis of the effectiveness of antitrust policy. There are two types of data one requires in order to perform such an analysis. One is data on the relevant market pre and post merger. The second is data on the specific predictions of the government agencies about the market post-merger. A key point of this article is to stress how weak an analysis of only the first type of data is. The frequent call for retrospective studies typically envisions relying on just this type of data, but the limitations on the analysis are not well understood. As I explain below, retrospective studies that ask whether prices went up post merger are surprisingly poor guides for analyzing merger policy. It is only when the second type of data is combined with the first type that a reliable analysis of antitrust policy can be carried out. There is a need both to collect the necessary data and to analyze it correctly. I. Introduction - The Need for Measures The antitrust policies of the United States should be reviewed periodically to make sure that the policies are promoting not impeding competition. The recent Antitrust Modernization Commission performed just such a function and concluded that U.S. antitrust policy was basically sound, though the report makes a number of recommendations for improvement. That report relied largely on the qualitative judgment of learned practitioners and scholars. Although the qualitative judgment of such people is important, it is no substitute for quantitative studies and measures. The dearth of such studies and measures means that there is no reliable guide for determining whether our antitrust policy is too lax in some areas and too stringent in others. I will concentrate my discussion about measures of antitrust policy effectiveness on merger policy because there are numerous merger investigations each year, and therefore a quantitative study of merger policy is possible, while that is not true of non-merger policy where at most a handful of cases are brought each year. I will focus on the mergers that the government chooses to investigate (e.g., those that receive a second request for information under the Hart-Scott-Rodino Act) and assume that the others raise no competitive concerns. This is of course, a simplification, but not an unreasonable one, especially for an initial analysis of the problem. In this article, I explain the inadequacy of our current state of knowledge regarding the effectiveness of antitrust policy. I then discuss the types of data that one must collect in order to be able to perform an analysis of the effectiveness of antitrust policy. There are two types of data one requires in order to perform such an analysis. One is data on the relevant market pre and post merger. The second is data on the specific predictions of the government agencies about the market post-merger. A key point of this article is to stress how weak an analysis of only the first type of data is. The frequent call for retrospective studies typically envisions relying on just this type of data, but the limitations on the analysis are not well understood. As I explain below, retrospective studies that ask whether prices went up post merger are surprisingly poor guides for analyzing merger policy. It is only when the second type of data is combined with the first type that a reliable analysis of antitrust policy can be carried out. There is a need both to collect the necessary data and to analyze it correctly. II. Why a Comprehensive Study of Antitrust is Needed Several commentators feel passionately that antitrust is too lax (e.g., New York Times) while some claim just the opposite (e.g.,Wall Street Journal), but passion is no substitute for evidence. By evidence I mean numbers or studies relying on quantitative data. Imagine that the Federal Reserve Board was trying to control the rate of inflation but did not have access to price statistics. Instead it relied on the opinions of a few non-randomly chosen shoppers about how fast they thought prices were rising. I suspect that the Fed would do a much poorer job of controlling inflation than it now does. Moreover, it is possible that in the absence of reliable quantitative information, monetary policy could be heavily influenced or could be perceived to be influenced by the ideological views of the people running the Federal Reserve Board. There are some data on antitrust but they mainly relate to the frequency of enforcement actions, such as the number of cases brought. Those numbers are often analyzed, yet knowing how many cases are brought tells one little about whether there are too few or too many cases brought, and whether the right cases are being brought. Unfortunately, the problem of figuring out what statistics to collect in order to determine whether antitrust policy is working well is a much harder problem than that facing the Fed in its price data collection efforts. We suggest below what statistics one should collect, and describe the type of analyses one could perform with such data. Surprisingly, the analysis is anything but straightforward. Simple tests, based on sensible intuition, turn out to be misleading, while slightly more refined tests work well. A fundamental question facing enforcement officials is whether their current merger policy is too lax or too stringent. This question is different from whether a particular merger enforcement decision was correct. It is rather asking whether overall the government is allowing too many or too few mergers. Specifically, is the government analysis of mergers systematically biased? The answer to this question requires one to identify the types of government analyses that are correct and those that are wrong and the circumstances that lead to the most errors. Because this question deals with overall policy, it can only be answered by systematically examining all (or a sample of) mergers. Determining whether in one particular case, the government turned out to be correct or not tells one very little about whether overall government policy should be altered. Indeed, even if the government policy is set exactly right, it would still be true that the government would make random errors in cases. Although it would be desirable to minimize such errors, it is not true that the presence of such errors indicates a systematic bias in policy. This last point, though perhaps obvious, often seems to get ignored when one hears the frequent calls for retrospective studies of past merger. Because it is an important point, I will highlight it and other key points by labeling them "Result". Result 0. A retrospective study of an individual merger tells the analyst nothing about whether there is a systematic bias in antitrust policy. At most, the analyst can learn whether a particular merger turned out to harm consumers. But, even that observation tells one little about whether the decision to allow the merger was a wise one based on the information available at the time of the merger. Even a merger that has a zero predicted price increase will turn out, for random reasons, to raise price about half the time. In the next section, I first discuss the types of measures that one might use to gauge the effectiveness of merger policy and the accuracy of the merger analysis that government agencies use. I then discuss biases that are likely to arise when analyzing such measures. Failure to use information about whether the mergers are challenged causes one to reach incorrect conclusions. This last point, which has to do with what economists call a self-selected sample, seems to have escaped notice and causes retrospective merger reviews to be quite imprecise guides to policy. Subsequent sections show how to apply the analysis to increasingly realistic settings. III. The Sample Selection Problem and How to Do the Analysis Correctly There are two types of data one needs to evaluate antitrust policy. The first is market data pre and post merger. The second is the enforcement agency's predictions of the merger. Any analysis of the data must account for the fact that the merger data one examines -- and, to repeat, I only look at mergers that have received a "second request" for more information -- already reflects a decision by the government agency about whether to challenge the merger. Virtually all of the data on mergers will represent mergers that the Department of Justice has decided not to challenge.(1) Therefore, as is now well understood since the work of Nobel Laureate James Heckman and others, the analysis based on such a sample may yield misleading results unless one explicitly understands the implications of how the sample is chosen. Let me explain. Suppose that a merger is proposed and that if the merger goes through the expected price change, ΔP, from the merger is drawn from some underlying probability distribution, ceteris paribus. (For simplicity, normalize the initial price to 100 so that ΔP can be thought of as a percentage price change. If the government agency knew this ΔP, then it would allow the merger if ΔP
If S > 0, the DOJ is systematically biased. It always overpredicts ΔP and therefore is too stringent in challenging mergers. If S 0, the DOJ is systematically biased in under-predicting ΔP, and is therefore too lax in allowing mergers. Consider the case where S = 0. The shaded part of Figure 1 indicates which mergers the government allows to go through unchallenged. Since all mergers in the shaded part have ΔP Result 1: If the government is unbiased (S = 0), retrospective studies of unchallenged mergers should be expected to indicate that on average post merger price falls. Similarly, if the government is too stringent (S > 0), an analysis of unchallenged mergers should be expected to indicate that post-merger prices fall, since the only unchallenged mergers are those with negative ΔP less than -S. Therefore, one cannot conclude that merger policy is too stringent merely from observing that post-merger prices fall. Result 2: If the government is too lax (S 0), then it is still quite possible that E(ΔP)0 where E(ΔP) is the expectation across all unchallenged mergers of ΔP conditional on a merger being unchallenged . Figure 1 The reason for Result 2 is easy to see in Figure 1. If the boundary between "allow" and "challenge" moves away from 0 and to the right (S 0)(3) , then it will still be the case that many unchallenged mergers will have ΔP 0. Only when S gets sufficiently large negatively will E(ΔP) > 0. We therefore have: Result 3: For a sufficiently biased policy (S 0) of laxity, E(ΔP)>0. The consequence of Results 1-3 is that retrospective studies of price change that focus on the average price change will not be a very good way of evaluating merger policy. It is correct that if one finds that ΔP is on average positive, then we know the government policy is too lax, but this is a very weak test. The reason is that we know from Result 2 that retrospective studies of price change can show negative price increases even if the government policy is too lax. A much better test of government bias would be to combine pre and post merger price data, ΔP, with the DOJ's predicted price changes, ΔPDOJ, and then explicitly calculate S. Notice that from the way (1) is set up, the estimate of S as the average of ΔPDOJ minus ΔP over all unchallenged mergers will precisely estimate S. We have: Notice that from the simple assumptions underlying equation (1), it follows that S is estimated correctly for each merger as ΔPDOJ - ΔP. The contrast between the precision in Result 4 and imprecision in Results 1 or 2 emphasizes why combining pre and post merger data with data on the enforcement agency's assessment is necessary to avoid the imprecision of Results 1 or 2. (In the next section, we show that the same type of results survives in a more realistic setting in which the bias is regarded as a random variable.) According to Result 1, one cannot conclude that antitrust policy is too stringent merely by observing whether price falls post-merger. According to Result 2, retrospective merger studies may fail to detect a lax antitrust policy because retrospective studies may show no price increase post merger. But Result 4 shows that a lax antitrust policy will be detected by more careful studies that combine pre and post merger data with data on the DOJ predictions at the time of merger.(4) IV. Evaluation of Antitrust Analyses The previous section explained the need to combine pre and post merger data with DOJ data on their evaluation of the merger. The discussion focused for simplicity only on price. But, of course, during the course of an investigation there are many types of analyses that are done. Each of them can be analyzed for their accuracy, as I now explain. In many merger investigations, considerations of entry, product repositioning, ability of buyers to vertically integrate, and predictions of price and market share from merger simulations are all used to guide the analysis. Yet we have few if any studies investigating the validity of any of these types of analysis. For example, suppose that in some of the unchallenged mergers, one finds that the reason for the government agency not challenging the merger is related to the likelihood of entry. We should test whether in fact entry turns out to be an important constraining effect on price. How often does entry occur in cases where it is alleged to be easy and therefore a tight constraint on price? When it does not occur, is that because price did not rise? Do government agencies too willingly accept claims that entry can constrain price? Similarly, in cases where the government relies on merger simulation, how well do the price predictions and market share predictions turn out? In cases where the government relies on product repositioning, does such repositioning in fact occur after the merger? How does the frequency of large buyers' using vertical integration as a means to protect themselves against price increases compare to the frequency of the government's reliance on vertical integration as a constraint on a merger's ability to raise price? Again, when it does not occur, is that because price did not rise? Without such studies, there is no way to judge and improve the analysis underlying most merger policy. In order to perform these types of studies, the DOJ at the end of each merger investigation should fill out a data sheet that summarizes each of their analyses, including price, entry, product and predictions, so that their predictions can be compared to actual industry behavior. Of course, one would have to account for how conditions post merger have changed (e.g., cost may have exogenously risen, demand conditions may have changed, product quality may have changed, etc.) and figure out how that would change the DOJ prediction, but that type of adjustment is routinely done in econometric studies. Such adjustments no doubt complicate the analysis, but are essential. V. Extension of Results — A More Realistic Model In this section, we show that our major results persist in a more realistic and complicated model of bias. We also discuss how to use a dataset on challenged mergers in addition to the dataset on unchallenged mergers.
Using the same notation as before, we previously defined S, the systematic bias, by the equation
Notice that in eq. (1), ΔPDOJ and ΔP are both expected prices not the actual price in the future. In fact, there will typically be many new events that occur between the time of the merger review when the predictions are formed and the time when the actual price is observed. For any particular merger, ceteris paribus, the relation between the actual price change, ΔP*, and the predicted is
where E is a random variable with expectation 0, independent of ΔP. If one can observe ΔP* for many mergers, then it follows that an estimate of the average ΔP will be given by the average of ΔP* across all mergers since the average of E will, in expectation, equal 0. The upshot is that the addition of E in (2) creates no estimation complications and the procedure described in the earlier section where we ignored E is a valid one for calculating expected price changes.(5) Eq. (1) has the unrealistic implication that the DOJ is off by exactly S in its expected price prediction in each merger. A more realistic model would allow for any systematic bias to be random across mergers, but to have a common average, S. For example, one can think of the DOJ being systematically biased upward in its price predictions on average, but on some mergers it is less so, while others it is more so. For example, one could think of the economist choosing one of many modeling techniques and that the randomness arises because the modeling techniques vary. We therefore, rewrite equation (1):
where The consequence of this more realistic set-up is that the simplicity of Figure 1 disappears (or is reduced) and a more sophisticated analysis is required. The reason the simplicity vanishes is because the set of unchallenged mergers will now be more complicated to determine than in Figure 1. For example, if s = 0, then under the previous assumptions, as Figure 1 shows, the set of all unchallenged mergers are those in the shaded area to the left of the ?P = 0 line. Now, however, it is possible that some merger where ΔP 0, may be challenged if the error The net effect is that unlike before where
where, fΔP = the probability density of ΔP, and Still assuming for illustration purposes that S = 0, it is straightforward to calculate where f
The following simple single numerical example illustrates the point. Suppose that s = 0, so that the DOJ is unbiased. Supposed that ΔP can take on one of two values with equal probability, $-5 or $10. In the absence of This example is meant to be illustrative only. However, it underscores the limitations of the inferences that one can draw about merger policy from retrospective studies. In the earlier analysis, we showed how a combination of pre and post merger data together with data from the DOJ analysis can provide a much better guide to assessing merger policy than retrospective studies alone. Does that remain true in the more sophisticated model? The answer is, yes, though with some caveats. For any proposed merger, it follows from (3) that
For mergers that are not challenged, we know that ΔPDOJ
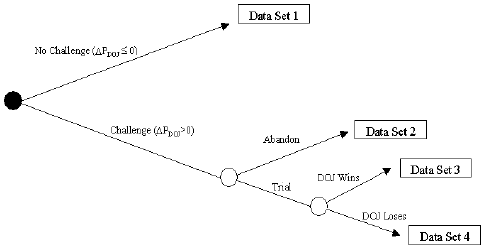
This means that for unchallenged mergers the upper tail of Figure 2 - Possible Outcomes
(b) Challenged Mergers-Another Self-Selected Sample Finally, we turn to another selected sample that we have so far ignored — namely those mergers that are challenged, go to court, and are allowed to proceed. To understand why this is the only other available data set for analysis consider Figure 2 which diagrams the major possible outcomes from merger investigations. If the DOJ predicts -- perhaps after a "fix" to the terms of the merger -- no price increase from the merger, (ΔPDOJ The set of mergers in dataset 4 results from unsuccessful court challenges is a self-selected sample, like dataset 1. It represents mergers that have the property that ΔPDOJ > 0. The analysis of dataset 4 has some similarities to that for dataset 1, though there is now the complication of the court's decision. In the case where the DOJ bias is non-stochastic (i.e., eq. (1)) and under the assumption that the court is unbiased, the court will allow a merger to proceed only if ΔPDOJ If we now add the complication that the bias, S + $\eta $, is stochastic with ? being random with mean 0, we obtain from eq. (3) that the challenged mergers that comprise dataset 4, have the property that (S + $\eta $) will tend to be above average. The reason is that for a challenged merger ΔPDOJ > 0 which implies ΔP + (S + $\eta $) > 0, or S + Finally, there may have been so few litigated cases that estimating S may suffer from small sample estimation problems. Although I have discussed analyzing dataset 1 and 4, I note that there are other sub-samples of the data that one might think of separately analyzing. I list a few suggestions below:
VII. Conclusion Without quantitative measures of the effectiveness of merger policy and of the accuracy of the government's analyses underlying merger policy, judgments about the appropriate antitrust policy will be based on qualitative information that can be subject to alternative interpretations. Merger policy can be an important force for either promoting or impairing competition. Merger policy is too important a policy to let it be set in the absence of detailed quantitative studies of its effects on price and other dimensions of competition. The government agencies should embark on such studies immediately and if they lack the authority to either collect the data or study it, they should seek it. Antitrust analysis of individual cases has gotten increasingly sophisticated. Evaluation of antitrust policy has not. There is a need to gather post merger industry data and a need to gather the predictions of DOJ merger analysis in order to evaluate whether U.S. policy and analysis can be improved. Strong opinions are not substitutes for quantitative analysis. Bibliography Antitrust Modernization Commission Report, 2007 Greene, William, Econometric Analysis, 2003 FOOTNOTES * University of Chicago; National Bureau of Economic Research. I currently serve as Deputy Assistant Attorney General, Antitrust Division, U.S. Department of Justice. I thank Thomas Barnett, Ken Heyer, Jeffrey Lien, Hill Wellford, and Gregory Werden for helpful discussions. These views do not necessarily reflect those of the United States Department of Justice. 1. We discuss in the next section how to use data on challenged mergers. For simplicity, I use the DOJ as the government agency responsible for mergers. What I say obviously applies also to the FTC. 2. With fixed cost of litigation, one might want to require a positive ΔP, but this is a detail for the point being made in the text. Indeed, the government can challenge a merger only if it "substantially" lessens competition. I am, for simplicity, assuming that the DOJ is using a consumer (not total) surplus standard. 3. If the government is lax (e.g., S = -5), then it will allow a merger where ΔP =$5. Hence, the boundary in Figure 1 between "challenge" and "allow" moves to the right to ΔP = $5. 4. In the absence of data on DOJ predictions, it might still be possible to estimate S. If one can observe ΔP for each unchallenged merger, then one can draw the distribution of ΔP. Under the assumptions in the text, the largest observed value of ΔP will equal - S. To see this, notice in Figure 1 that the line ΔP = -S is the dividing line between the area labeled "challenge" and "allow" when S 5. The addition of a stochastic component, E, means that the procedure to estimate S described in Footnote 4 needs to be modified slightly. The actual distribution of ΔP* for unchallenged mergers is a mixture of the distribution of ΔP (truncated at ΔP = -S) and the distribution of E. Under certain assumptions on the distributions, one can estimate the (truncated) distribution of ΔP and then estimate S as max -ΔP. 6. If one is willing to define a distribution on 7. The group of unchallenged mergers that have been "fixed" might be an interesting one to study separately. 8. A more complicated model for dataset 1 could analyze the decision of the merging parties to settle (fix the case or abandon it) based on what their estimates of winning in court are. This would provide additional information to estimate S. |

 U.S. Department
of Justice
U.S. Department
of Justice
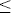 0 and would challenge the merger if ΔP > 0. This would be the optimal merger policy.
0 and would challenge the merger if ΔP > 0. This would be the optimal merger policy.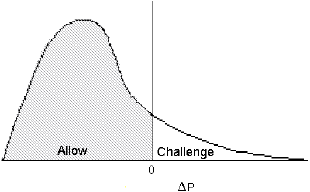
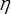 ,
,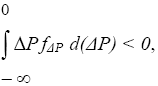
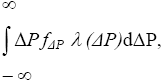
 (ΔP) = probability a merger with actual predicted price increase of ΔP will go unchallenged.
(ΔP) = probability a merger with actual predicted price increase of ΔP will go unchallenged. 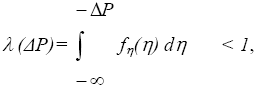
 , of S will have the property that E(
, of S will have the property that E(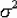 ,
,
 O. Because ΔP is an expectation not an actual value, the method just described needs to be adjusted slightly. I discuss this adjustment in Section 4. Estimating S as described in the text is likely to produce more accurate estimates of S since it utilizes more data.
O. Because ΔP is an expectation not an actual value, the method just described needs to be adjusted slightly. I discuss this adjustment in Section 4. Estimating S as described in the text is likely to produce more accurate estimates of S since it utilizes more data.